Теорема о медианах треугольника
Рассмотрим произвольный треугольник АВС.
teorema_o_medianah_treugolnikama – медиана треугольника, проведенная к стороне BC
mb – медиана треугольника, проведенная к стороне AC
mc– медиана треугольника, проведенная к стороне AB
O – центр пересечения медиан треугольника
A, B, C – вершины треугольника
Теорема о медианах треугольника формулируется следующим образом: медианы треугольника пересекаются в одной точке (на рисунке точка O) и делятся этой точкой в пропорции 2:1, если считать от вершины, с которой проведена медиана.
Все формулы по теме теорема о медианах треугольника:
Основные формулы
Формулы площадей
Формулы объемов
Формулы периметра
Геометрические фигуры
Объемные тела
Площадь поверхности
Тригонометрические формулы
Теоремы по геометрии
Теорема Пифагора
Обратная теорема Пифагора
Теорема косинусов
Теорема синусов
Теорема тангенсов
Теорема о медианах треугольника
Теорема о биссектрисе
Теорема о сумме углов треугольника
Теорема о сумме углов многоугольника
Теорема Чевы
Теорема Виета
Теорема Фалеса
![+ , - , \cdot , : , x^n , \sqrt[n]{x} и \log_a{x}](/tpl/images/0480/8307/7c93b.png) – имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении
– имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении 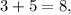 а у другого
а у другого 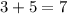 :–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что
:–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что 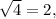 но одновременно с тем как бы и
но одновременно с тем как бы и 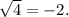 Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно
Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно 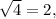 и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.
и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.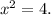 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять:  и
и 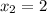 или в короткой записи
или в короткой записи 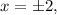 что равносильно
что равносильно 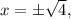 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 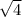 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения:
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения: 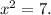 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять: 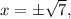 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 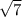 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.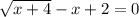 ;
;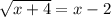 ;
;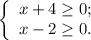
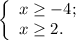
![x \in [ 2 ; +\infty ]](/tpl/images/0480/8307/22de1.png) ;
;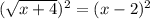 ;
;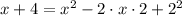 ;
;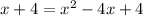 ;
;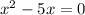 ;
;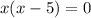 ;
;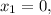 это не соответствует ОДЗ, поскольку
это не соответствует ОДЗ, поскольку ![x_1 = 0 \notin [ 2 ; +\infty ]](/tpl/images/0480/8307/72ba8.png) ;
;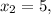 что соответствует ОДЗ, поскольку
что соответствует ОДЗ, поскольку ![x_2 = 5 \in [ 2 ; +\infty ]](/tpl/images/0480/8307/2f42f.png) ;
;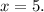
ответ: