Задание 1 Даны координаты вершин некоторого треугольника A (-10; 4); B (2; -12); C (5; 9). Требуется найти а) периметр треугольника ABC; б) уравнения сторон; в) уравнения медианы AM; г) уравнение высоты AH; д) уравнение прямой, проходящей через точку А, параллельно прямой ВС. 2 Написать каноническое уравнение окружности, имеющей диаметр АВ. 3 Написать каноническое уравнение параболы, проходящей через точку А симметрично относительно оси абсцисс для вариантов с четным номером и симметрично относительно оси ординат для задач с нечетным номером.
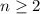равных частей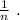
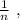нужно разрезать верёвочку длины 2 на 
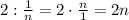частей.
частей.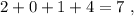
не делится на три.
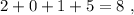не делится на три.
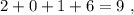делится на три!
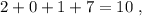не делится на три.
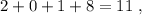не делится на три.
Система не имеет решений, значит графики не пересекаются.
Графики не пересекаются, значит прямые параллельны.
Надо ответить на вопрос, когда прямые параллельны.
Когда их коэффициенты при х и у пропорциональны
2:1=(-1):а
а=-0,5
Но параллельные прямые могут совпасть, чтобы этого не случилось, надо чтобы отношение свободных коэффициентов не было пропорционально отношению коээфициентов при х и у.
В нашем случае это так
2:1≠5:2
ответ. а=-0,5