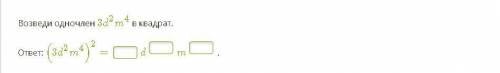
Двузначное число, где а десятков и b единиц представим в виде 10a+b (это разложение числа по разрядам). Далее записываем условие задачи: 1) первое предложение
(10a+b):(a+b)=7(ост.3)
10a+b=7(a+b)+3
10a+b=7a+7b+3
3a-6b=3
a-2b=1 - это первое уравнение системы.
2) читаем второе предложение задачи
При перестановке цифр данного двузначного числа получим число 10b+a. Известно, что оно на 36 меньше, чем число 10a+b. Запишем это: 10a+b-36=10b+a
9a-9b=36 |:9
a-b=4 - это второе уравнение системы
Решаем систему:
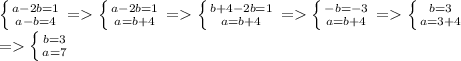
Итак, искомое двузначное число равно 73.
1) M = {11k + 7, где к = 1,2,3,4,5,6,7,8} = {11,18,25,32,39,46,53,60,67,74,81,88}
2) М = n^2, n = 1,2,3,...,9. M = {квадраты всех чисел от 1 до 9}
3) (x,y,z), где x - 1-я монета, y - 2-я монета, z - 3-я монета: x+y+z < 6 => среди x, y и z не может быть ни одной 5-ки, а также больше двух двоек.
a) Ноль двоек: (1,1,1) b) Одна двойка: (1,1,2),(1,2,1),(2,1,1) c) Две двойки: (1,2,2),(2,1,2),(2,2,1). Итак: (1,1,1),(1,1,2),(1,2,1),(2,1,1),(1,2,2),(2,1,2),(2,2,1)
4) (x,y), где x - число очков выпавших на 1-й кости, y - число очков выпавших на 2-й кости: |x-y| < 2 => (1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),(5,4),(5,5),(5,6),(6,5),(6,6) - все пары (x,y) такие, что |x-y| < 2. Всего таких пар n = 16.
5) Двухзначные числа: 10,11,12,13,...,99. Всего таких чисел N = 99-10 = 89. Двухзначные числа, которые делятся на 13: m = 13k, k = 1,2,3,4,5,6,7. Всего таких чисел n = 7. Отсюда, искомая вероятность p = 7/89
9d^4m^8
Объяснение:
Цифры после стрелочки это степень буквы