1(2б) Подати вираз у вигляді многочлена: 1) (5х + 8у)(8у – 5х),
2) (3х - 2у)2.
2(2б) Розкласти на множники:
1) 36 - 81b2,
2) 64n2 - 80nq + 25q2.
3(2б)Обчисліть, використовуючи формули скороченого множення:
1) 0,972 – 0,032
2) 1372 - 2 137 47 + 472
4(2б) Спростити вираз (х - 2)(х+2) - (х – 5)2 .
5(2б) Розв’язати рівняння
100 - 9х2 = 0;
36х2 - 60х + 25 = 0.
6(2б)Спростити вираз
(2 - a)(2 + a)(4 + a2) + (6 - a2)2 і знайти його значення, якщо a = -12.
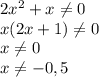
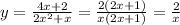
b1*(1+q+q²+q³)=6
b1²*(1+q²+q⁴+q⁶+)=12
Возведём первое уравнение в квадрат:
b1²*(1+q+q²+q³)²=36
b1²*(1+q²+q⁴+q⁶+)=12
Разделив теперь первое уравнение на второе, придём к уравнению относительно q: (1+q+q²+q³+)²/(1+q²+q⁴+q⁶+)=3. Но в скобках числителя - бесконечная геометрическая прогрессия со знаменателем q, её сумма S2=1/(1-q). В скобках знаменателя - бесконечная геометрическая прогрессия со знаменателем q², её сумма S3=1/(1-q²). Отсюда следует уравнение (1-q²)/(1-q)²=3, которое приводится к квадратному уравнению 2*q²-3*q+1=0. Решая его, находим q1=1 и q2=1/2. Но при q=1 сумма прогрессии была бы равна бесконечности, поэтому q=1/2. ответ: 1/2.