
![5)f(x)=(x+1)^{2} Cos2x\\\\f'(x)=[(x+1)^{2}]'*Cos2x+(x+1)^{2}*(Cos2x)'= \\\\=2(x+1)*Cos2x-(x+1)^{2}*2Sin2x=2[(x+1)Cos2x-(x+1)^{2}Sin2x)]\\\\f''(x)=2[(x+1)'Cos2x+(x+1)*(Cos2x)'-[(x+1)^{2}]'Sin2x-(x+1)^{2}(Sin2x)']=\\\\=2[Cos2x-2(x+1)Sin2x-2(x+1)Sin2x-(x+1)^{2}*2Cos2x]=\\\\=2(Cos2x-4(x+1)Sin2x-2(x+1)^{2}Cos2x)](/tpl/images/1577/9133/e4a35.png)
![6)f(x)=xCos(x^{2}+1)\\\\f'(x)=x'*Cos(x^{2}+1)+x*(Cos(x^{2}+1))'=Cos(x^{2}+1)-x*2xSin(x^{2}+1)=\\\\=Cos(x^{2}+1)-2x^{2} Sin(x^{2}+1)\\\\f''(x)=[Cos(x^{2}+1)]'- 2[(x^{2})'*Sin(x^{2}+1)+x^{2}*(Sin(x^{2}+1))'] =\\\\=-2xSin(x^{2}+1)-2(2xSin(x^{2}+1)+2x^{3}Cos(x^{2}+1)=\\\\=-2xSin(x^{2}+1)-4xSin(x^{2}+1)-4x^{3}Cos(x^{2}+1)=\\\\ -6xSin(x^{2}+1)-4x^{3}Cos(x^{2}+1)](/tpl/images/1577/9133/2e065.png)
5)
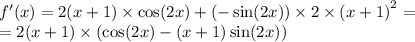
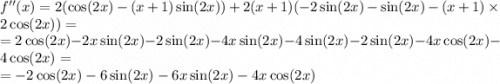
6)
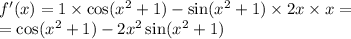
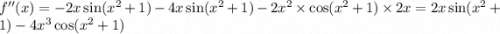
В решении.
Объяснение:
Решить систему неравенств:
1) (7,4х + 23)/21 <= 1 + 0,4x
3x - 5 <= (20x - 31)/7
Умножить обе части первого неравенства на 21, а второго на 7, чтобы избавиться от дробного выражения:
7,4х + 23 <= 21(1 + 0,4x)
7(3x - 5) <= 20x - 31
Раскрыть скобки:
7,4x + 23 <= 21 + 8,4x
21x - 35 <= 20x - 31
7,4x - 8,4x <= 21 - 23
21x - 20x <= -31 + 35
-x <= -2
x <= 4
x >= 2 (знак неравенства меняется при делении на -1)
x <= 4
Решение первого неравенства х∈[2; +∞);
Решение второго неравенства х∈(-∞; 4];
Решение системы неравенств [2; 4], пересечение.
Неравенства нестрогие, скобка квадратная, а знаки бесконечности всегда с круглой скобкой.
Натуральные числа: 2; 3; 4 (2 и 4 входят в решения системы).
2) 1 - 2х <= (28 - 53x)/27
0,1x + 3 < (13 - 0,7x)/3
Умножить обе части первого неравенства на 27, а второго на 3, чтобы избавиться от дробного выражения:
27(1 - 2х) <= 28 - 53x
3(0,1x + 3) < 13 - 0,7x
Раскрыть скобки:
27 - 54х <= 28 - 53x
0,3x + 9 < 13 - 0,7x
-54x + 53x <= 28 - 27
0,3x + 0,7x < 13 - 9
-x <= 1
x < 4
x >= -1 (знак неравенства меняется при делении на -1)
x < 4
Решение первого неравенства х∈[-1; +∞);
Решение второго неравенства х∈(-∞; 4);
Решение системы неравенств [-1; 4), пересечение.
Первое неравенство нестрогое, скобка квадратная, второе - строгое, скобка круглая, а знаки бесконечности всегда с круглой скобкой.
Натуральные числа: 1; 2; 3 (4 не входит в решения системы).
1. Разложите на множители:
1)m³+125n³=m³+(5n)³=(m+5n)(m²-5mn+25n²)
2)-5x²+30x-45=-5(x²-6x+9)=-5(x-3)²
3)10000-c⁴=10⁴-c⁴=(10+c)(10³-10c²+10c²-c³)=(10+c)(10²(10-c)+c²(10-c))=(10+c)(10-c)(10²+c²)
2. Упростите выражение:
b(b - 3)(b + 3) – (b – 1)(b² + b + 1)=b(b²-9)-(b³-1)=b³-9b-b³+1=-9b+1
3. Разложите на множители:
1)3y³ - 36y² + 108y = 3y(y² - 12y + 36) = 3y(y - 6)² = 3y(y - 6)(y - 6)
2)a² + 8ab + 16b² - 1 = (a² + 8ab + 16b²) - 1 = (a + 4b)² - 1 = (a + 4b - 1)(a + 4b + 1)
4. Решите уравнение:
1)3x^3-108x=0
3x(x^2-36)=0
3x(x-6)(x+6)=0
3x=0
x=0
ответ:x=0
2)121x^3-22x^2+x=0
x(121x^2-22x+1)=0
x(11x-1)^2=0
x=0
ответ:x=0
5. Докажите, что значение выражения - делится нацело на 22:
3⁹-5³=(3³)³-5³=(3³-5)((3³)²+3³*5+5²)=(27-5)*(3⁶+3³*5+25)=22*(3⁶+3³*5+25).
значит 3⁹-5³ делится на 22.