пусть а - сторона основания, а l - апофема, тогда формула площади поверхности конуса равна
Подставим вместо а и S их значения и найдем апофему l
Через апофему проведем сечение пирамиды. В сечении получаем равнобедренный треугольник, основание которого равно стороне а=5, а боковые стороны апофеме l=6. Угол между боковой стороной треугольника и его основанием и есть угол наклона боковой грани пирамиды к плоскости основания. Найдем его, проведем высоту в равнобедренном треугольнике к его основанию. Высота равнобедренного треугольника, проведенная к основанию является так же его биссектрисо и медианой. Поэтому она делит равнобедренный треугольник на два равных прямоугольных треугольника. Найдем косинус искомого угла из прямоугольного треугольника.
Cos A=2,5/6=25/60=5/12 Отсюда следует, что угол наклона боковой грани к плоскости основания пирамиды равен arccos (5/12)
Квадратные уравнения решаются очень легко. Самый классический их решения, через дискриминант.
Во первых надо знать, что Квадратное уравнение имеет 2 корня (основная теорема алгебры).
Во вторых надо знать, что если число (дискриминант) под корнем отрицательно, то решения у уравнения нет.
В общем виде, квадратное уравнение выглядит так:
При этом , так как уравнение обращается в линейное.
Поначалу находят дискриминант: Если уравнение не имеет решений (вообще имеет, но это в школе не проходят). Если то уравнение имеет 1 решение (корень). Если - уравнение имеет 2 корня.
После того как ты нашел сам дискриминант, используешь следующую формулу:
пусть а - сторона основания, а l - апофема, тогда формула площади поверхности конуса равна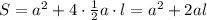
Подставим вместо а и S их значения и найдем апофему l
Через апофему проведем сечение пирамиды. В сечении получаем равнобедренный треугольник, основание которого равно стороне а=5, а боковые стороны апофеме l=6. Угол между боковой стороной треугольника и его основанием и есть угол наклона боковой грани пирамиды к плоскости основания. Найдем его, проведем высоту в равнобедренном треугольнике к его основанию. Высота равнобедренного треугольника, проведенная к основанию является так же его биссектрисо и медианой. Поэтому она делит равнобедренный треугольник на два равных прямоугольных треугольника. Найдем косинус искомого угла из прямоугольного треугольника.
Cos A=2,5/6=25/60=5/12 Отсюда следует, что угол наклона боковой грани к плоскости основания пирамиды равен arccos (5/12)