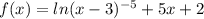
сначала задача: примем за х первоначальную стоимость товара, после повышения цены на 10% товар стал стоить (1+0,1)x = 1,1x потом цена быласнижена на 10% тоесть стала 1,1x - 1,1x*0,1 = 1,1x -0,11x=0,99x
нам сказано что после снижения цены товар стал стоить 1089 рублей, то есть 0,99х = 1089 ; х=1089/99*100=1100 рублей.
ответ: первоначальная стоимость товара = 1100 рублей
Теперь уравнение: x^2+5x=0; решается путём выноса общего множителя за скобку, в данном случае общий множитель это х(икс),его и вынесем. и получим х(х+5)=0
произведение двух множителей = 0 тогда, когда хотябы 1 множитель = 0
то есть
х=0 или х+5=0
х=0 или х=-5
ответ: 0;-5
Наименьшее значение функции - 13.2501054 или ln(0.5)^-5 + 19.5 в точке x = 3.5.
Объяснение:
Функция принимает своё максимальное(минимальное) значение тогда, когда производная функции равна 0.
f'(x) =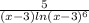
+ 5 = 0
Корней нет, найдём значение функции на краях отрезка
При x = 3.5
f(3.5) = ln(0.5)^-5 + 5*3.5 + 2 ≈ 13.2501054 - локальный минимум
f(7) = ln(4)^-5 + 35 + 2 ≈ 37.1953092 - локальный максимум
Наименьшее значение функции - 13.2501054 или ln(0.5)^-5 + 19.5 в точке x = 3.5.