Тангенс угла наклона касательной равен производной в точке касания к графику функции.
tgα = y'(x).
1) y = 0,2x^2 + 2x - 4, A(2; 0,8).
Проверяем - принадлежит ли точка данной функции.
0,2*2² + 2*2 - 4 = 0,8. Да, принадлежит.
Находим производную: y' = 0,2*2x + 2.
y'(2) = 0,2*2*2 + 2 = 2,8.
ответ: tgα = 2,8.
2) y = -3x^2 - x + 5, А(-2; -5).
Аналогично проверяем - точка А на кривой (парабола).
y' = -6x - 1,
y'(-2) = -6*(-2) - 1 = 12 - 1 = 11.
ответ: tgα = 11.
3) y = (x^2 - 1)/(x - 5), A(3; 3 2/3). (Ели так дано задание)
В этой задаче сложное решение, так как точка А не лежит на кривой.
Производная : y' = (2x(x - 5) - 1*(x^2 - 1))/(x - 5)^2) = (x^2 - 10x + 1)/((x - 5)^2).
Производная в точке касания хо: (xо^2 - 10xо + 1)/((xо- 5)^2).
Получим уравнение касательной проходящей через точку A(3;3 2/3):
3 2/3 = ((xо^2 - 10xо + 1)/((xо- 5)^2))(3 - хо) + ((xо^2 - 1)/(xо - 5)).
Решение затруднено, так функция - кубическая.
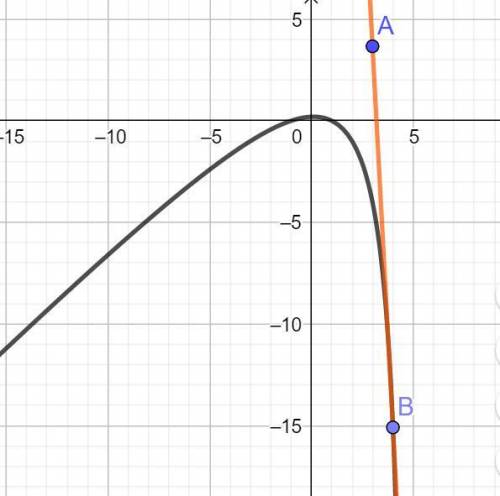
Ориентировочно решение найдено графически в программе ГеоГебра: у = -18,76х + 59,95.
График приведен во вложении.
1) 1:5 - это масштаб уменьшения,т.е. если длина детали 2,1 см, то ее реальная длина будет равна 5*2,1 = 10,5 см
3:1 - это масштаб увеличения, т.е. если реальная длина равна 10,5 см, то длина детали в этом масштабе будет равна 3*10,5 = 31,5 см
2) а - сторона квадрата
d - диаметр окружности
r - радиус окружности
т.к. а = d, то r = a/2 = 4/2 = 2cм
Sфигуры = Sквадрата + 2Sполуокружностей = Sквадрата + Sокружности = a^2 + Пr^2 =
= 4^2 + 3,14*2^2 = 28,56 см^2
Pфигуры = 2Lполуокружностей + 2стороны квадрата = Lокружности + 2a = 2Пr + 2a =
= 2*3,14*2 + 2*4 = 20,56 см
3) x - число туристов, y - число автобусов
"Группу туристов можно рассадить в 40-местные автобусы так, что в автобусах свободных мест не останется":
x = 40y
"В связи с тем, что вместо 40-местных были поданы 34-местные автобусы, пришлось заказать на два автобуса больше. При этом в одном из автобусов 14 мест оказались свободными.":
x = 34(y + 2) - 14
40y = 34(y + 2) - 14
40y = 34y + 68 - 14
6y = 54
y = 9 - автобусов
х = 40*9 = 360 туристов
Привет. Скачай приложение photo match он все приклади решает