Шоколадка стоит 80 р.
Объяснение:
Предположим, что
шоколадка - y
конфета - х
орео - 5х (так как в пять раз дороже)
Лёня купил на одно орео и 3 конфеты больше, чем Саша. Значит если от 770 рублей отнять 530 рублей (770 - 530 = 240), мы узнаем цену одного орео с 3 конфетами. То есть: 5x + 3x = 240, 8x = 240, x = 30 рублей.
Чтобы узнать цену шоколадки, нам нужно вместо х подставить 30 рублей. Возьмем для этого Сашин "набор" покупок.
10x (2 орео) + y (шоколадка) + 5х (5 конфет) = 530 р.
10*30 + y + 5*30 = 530
300 + y + 150 = 530
y = 530 - 300 - 150
y = 80 рублей
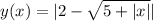
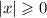


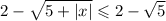

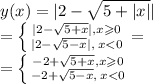
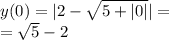
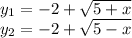
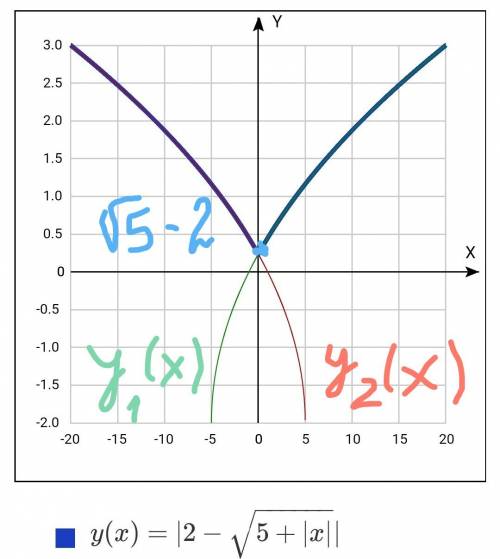
Объяснение:
Графиком будет прямая проходящая через точки (0;-2) и (0,5;0)
Чтобы арифметически узнать проходит ли график через какую-то точку, вместо х и у подставляем координаты данной точки:
-5 = -1* 4 -2
-5 = -6, тк тождество неверно, то график функции у = 4х -2 не проходит через данную точку