ОТДАМ ВСЕЕЕ Представьте в виде многочлена выражение: a).-3a(2a-b); б) 2x2y(4x3+5xy?-y?); b)(x-2)(2x+3); г)(у+3)(у?+у-6) 2. Разложите на множители: a)12a2b3-18a5b2; б) (b2-7)2-b(b2-7); b) 8х+8у-ах-ау; г) 8m7-6v2n-12m5n3+9n4. 3. Решите уравнение: a)(3x-5)(2x+7)=(3x+1)(2x-3)+4x б) 10x2-5x=0
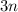
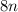
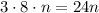
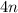
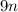
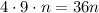
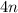
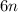

![[4,6]=2\cdot 2\cdot 3=12](/tpl/images/0629/9227/9a182.png)
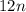
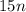
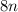
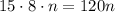
9y² + 12xy практически создают квадрат суммы, дополним это выражение:
9y² + 12xy + 4x² = (3y + 2x)², заметим, что это выражение есть целое число в квадрате.
5x² + 12xy + 9y² + 6x + 34 = x² + (4x² + 12xy + 9y²) + 6x + 34 = (3y + 2x)² + x² + 6x + 34
x² + 6x также дополняем до полного квадрата:
x² + 6x + 9 = (x + 3)²
(3y + 2x)² + x² + 6x + 34 = (3y + 2x)² + x² + 6x + 9 + 25 = (3y + 2x)² + (x + 3)² + 25
25 = 5² (целое число в квадрате)
(3y + 2x)² + (x + 3)² + 25 = (3y + 2x)² + (x + 3)² + 5²
Итак, получившееся выражение однозначно при любых целых x и y можно представить в виде суммы квадратов трёх натуральных чисел.