![1)\ \ |2x^2-5x|-3=0\\\\a)\ \ 2x^2-5x\geq 0\ \ \to \ \ x(2x-5)\geq 0\ \ ,\ \ x\in (-\infty ;0\, ]\cup [\, 2,5\ ;+\infty \, )\\\\2x^2-5x-3=0\ \ ,\ \ x_1=-0,5\ \ ,\ \ x_2=3\\\\b)\ \ 2x^2-5x](/tpl/images/1582/1659/4b921.png)
![2)\ \ |x^2-7x+5|=1\\\\a)\ \ x^2-7x+5\geq 0\ \ \to \ \ \ x\in \Big(-\infty ;\dfrac{7-\sqrt{29}}{2}\ \Big]\cup \Big[\ \dfrac{7+\sqrt{29}}{2}\ ;+\infty \, \Big)\\\\x\in (-\infty \, ;\, 0,81\ ]\cup [\ 6,19\ ;+\infty \, )\\\\x^2-7x+5=1\ \ ,\ \ x^2-7x+4=0\ ,\\\\D=33\ \ ,\ \ x_{1,2}=\dfrac{7\pm \sqrt{33}}{2}\ \ ,\ \ x_1\approx 0,63\ ,\ x_2\approx 6,37\\\\b)\ \ x^2-7x+5](/tpl/images/1582/1659/76d82.png)
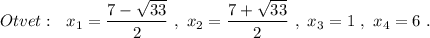
(х-2)(х+3)/(х-4)>=0
x^2+3x-2x-6/x-4 >=0
x^2-x-6/x-4 >=0
x^2-x-6=0
d=1+24=25=5^2
x1=1+5/2=3
x2=1-5/2=-2
x^2-x-6=(x-3)(x+2)>=0
x принадлежит (-бесконечности: -3] в обьединении [2;+бесконечности)
х принадлежит (4:+бесконечности)
обьединяем
х принадлежит (4:+бесконечности)
х(х+1)(х-1)/(x+2)(х-2)>=0
(x^2+x)(x-1)/(x+2)(х-2)>=0
x^3-x^2+x^2-x/(x+2)(х-2)>=0
x(x^2-1)/(x+2)(х-2)>=0
x принадлежит (-бесконечности: -1] в обьединении [1:+бесконечности)
x принадлежит(-бесконечности: -2) в обьединении (2:+бесконечности)
обьединяем
х принадлежит(-2:-1] в обьединении [1;2)
квадратные скобки значат что значение включается в промежуток, круглые не включают