Рассмотрим систему уравнений
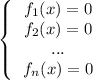
Каждое уравнение системы определяет на плоскости некоторое множество точек A1, A2, ..., An (может быть пустое или одну точку или бесконечно много точек). Решением систему уравнений называют пересечение всех этих множеств, то есть
A= A1 ∩ A2 ∩ ... ∩An.
Если
1) множество A состоит только из одной точки, то система уравнений имеет одно решение;
2) множество A пустое, то система уравнений не имеет решений;
3) множество A состоит из бесконечно много точек, то система уравнений имеет бесконечно много решений.
В частном случае можем рассмотреть систему линейных уравнений:
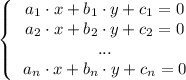
в которой, каждое из уравнений системы определяет на плоскости некоторую прямую.
Тогда возможны случаи:
1. Если все прямые совпадают, то система имеет бесконечное количество решений - так как в этом случае точек пересечений бесконечно много.
2. Если хотя бы 2 прямые системы параллельны, то есть не совпадают, то система не имеет решения - так как в этом случае нет точки пересечения.
3. Если все прямые имеют одну точку пересечения, то система имеет одно решение.
После первого, второго и третьего переливания в первом, втором и третьем сосудах осталось 1/2, 2/3 и 3/4 воды, имевшейся в каждом из этих сосудов до переливания.
Тогда в третьем сосуде перед последним переливанием было 12 : 3/4 = 16 (л) воды, из него отлили 16 – 12 = 4 (л) воды, а в первом сосуде до последнего переливания было 12 – 4 = 8 (л) воды.
Во втором сосуде перед вторым переливанием было 12 : 2/3 = 18 (л) воды, из него отлили
18 – 12 = 6 (л) воды, а в третьем сосуде до второго переливания было 16 – 6 = 10 (л) воды.
В первом сосуде перед первым переливанием было 8 : 1/2 = 16 (л) воды, из него отлили
16 – 8 = 8 (л) воды, а во втором сосуде до первого переливания было 18 – 8 = 10 (л) воды.
ответ. 16, 10 и 10 л.