


1) отрицательное,т,к при умножение 2-х чисел в разными знаками,прооизведение отрицательное
2) положительное,так как при деление двух чисел с одинаковыми знаками частное положительное
3)отрицательное,приведем показатели степени в общему знаменателю
получим 42 в степени 9/21 53 в степени 14/21
второе число большее,поэтому и знак будет минус
4)отрицательное т,к
1 представим,как 2в степени 0.получим,что второе опять больше первого
5)положительное,так как при сложение 2-х полодительный сумма положительная

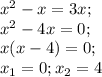
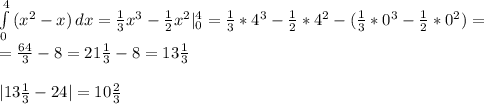
Длина забора, а именно 230 метров, является периметром участка, который можно записать как:
230 = 2 * (а + в).
Площадь участка записываем следующей формулой:
3250 = а * в.
Находим сумму двух сторон участка.
Делим периметр на 2.
а + в = 230 / 2 = 115 м.
а + в = 115.
Выражаем а.
а = 115 - в.
Подставляем данное значение в формулу площади.
(115 - в) * в = 3250.
115 * в - в^2 - 3250 = 0.
в^2 - 115 * в + 3250 = 0.
Д^2 = (-115)^2 - 4 * 1 * 3250 = 13225 - 13000 = 225.
Д = 15.
а = (115 + 15) / 2 = 130 / 2 = 65 м.
в = 115 - 65 = 50 м.
65 и 50 метров.
1. Пусть Х часов - время, которое необходимо одному из подъемных кранов разгрузить баржу.
Обозначим за 1 - весь объем работ.
Тогда 1/Х ед/час - производительность этой баржи.
2. Известно, что второй кран разгрузит баржу на 3 часа быстрее, то есть за (Х + 3) часа.
Тогда его производительность 1/(Х + 3) ед/час.
3. В задаче сказано, что при совместной работе им потребовалось бы 6 часов 40 минут или 20/3 часа.
Тогда совместная производительность 1 / 20/3 = 3/20 ед/час.
4. Получили уравнение.
1 / Х + 1 / (Х + 3) = 3/20.
(2 * Х + 3) * 20 = 3 * Х * (Х + 3).
3 * Х * Х - 31 * Х - 60 = 0.
Дискриминант D = 31 * 31 + 12 * 60 = 1681.
Х = (31 + 41)/ 6 = 72 / 6 = 12 часов - первому крану.
12 + 3 = 15 часов - второму.
ответ: Первому крану потребуется 12 часов, второму - 15 часов.
х - скорость первого поезда
у - скорость второго поезда
3х+3у=270
3(х+у) =270
х+у=90
х=90-у
270/х - 270/у = 27/20 (27/20 часа это 1 час 21 минута)
270 (1/(90-у) - 1/у) = 27/20
1/(90-у) - 1/у = 1/200
у"+310у-18000=0
D=96100+72000=168100
у=(-310+410)/2 = 50
х=40
ответ: скорость первого поезда 40 км/час, скорость второго поезда 50 км/час.
Объяснение: