
ответ:: S6 = 10,2
Объяснение:
1. Для определения суммы шести членов арифметической прогрессии необходимо узнать значение шестого ее члена и только тогда найти S6 по формуле
Sn = (a1 + an) : 2 * n.
2. Известна формула для энного члена арифметической прогрессии
аn = a1 + d *(n - 1).
3. Пользуясь этой формулой вычислим разность прогрессии d.
a4 = a1 + d * 3;
1,8 = 1,2 + 3 d;
d = (1,8 - 1,2) : 3 = 0,6 : 3 = 0,2.
4. Теперь найдем а6.
а6 = а1 + d * 5 = 1,2 + 0,2 * 5 = 1,2 + 1 = 2,2.
5. Отвечаем на во задачи
S6 = (a1 + a6) : 2 * 6 = (1,2 + 2,2) : 2 * 6 = 10,2.
27.
Объяснение:
Пусть х - цифра из разряда десятков неизвестного двузначного числа,
у - цифра из разряда единиц этого числа,
тогда неизвестное двузначное число можно записать в виде:
(10х + у).
Утроенная сумма цифр этого числа будет иметь вид: (3(х + у)). =>
3(х + у) = 10х + у
Если поменять местами цифры искомого двузначного числа, то получим число: (10у + х). =>
10у + х - 45 = 10х + у.
Решим систему уравнений:
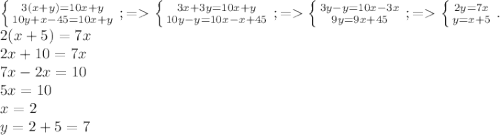
27 - искомое двузначное натуральное число.
Проверка:
3(2 + 7) = 27
3 * 9 = 27
27 = 27
72 - 27 = 45
2. Пусть х-1-ый день
х-5 - км 2-ой день
3 день
3/7 * (х+х-5)
всего х+х-5 + 3/7 * (2 х-5) = 110
14 х-35+6 х-15=770
20 х=720
х=36 - 1 день
36-5=31 - 2 день
110-36-31=43 - 3 день
1. Принимаем за х расстояние, которое пешеход до встречи.
(17 - х) км проехал велосипедист до встречи.
2. 15 минут = 15/60 часа = 0,25 часа.
3. Составляем уравнение и решаем его:
х/4 - (17 - х)/12 = 0,25;
(12х - 68 + 4х)/48 = 0,25;
16х = 80;
х = 5.
Велосипедист проехал от города до места встречи 17 - 5 = 12 км.
ответ: пешеход до места встречи 5 километров, велосипедист проехал 12 километров.