Периметр прямоугольника равен 56 см. Какими должны быть размеры его сторон, чтобы площадь прямоугольника была наибольшей? Стороны прямоугольника должны быть (?)см и (?) см
Максимально возможная площадь прямоугольника при данном периметре равна (?) см2.
1) Простое уравнение y - скорость грузовика (x + 20) - скорость авто тогда: (x+20)* 5 = x*7 5x + 100 = 7x 100 = 7x- 5x 2x = 100 x = 50 - скорость грузовика Расстояние равно 50 * 7 = 350
2) x - скорость течения, тогда : (4+x) скорость лодки по течению (4-x ) скорость лодки против течения (4+x)*2,4 = 1,2 + (4-x)*4.8 9.6 + 2.4x = 1.2 + 19.2 - 4.8x 2.4x+4.8x = 19.2+1.2-9.6 7.2x= 10.8 x = 1.5 км/ч
Метод алгебраического сложения заключается в том, чтобы вычитая или же суммируя уравнения системы получить 1 уравнение с 1 неизвестным. Для этого в данном примере можно умножить первое уравнение на 3 с обеих сторон (заметим, что при этом значения неизвестных не изменятся, то есть полученное уравнение будет эквивалентно исходному). После этой операции система будет иметь такой вид:
Теперь, если отнимем от первого уравнения системы второе, то получим следующее: Как видите, мы получили уравнение с 1 неизвестным. Отсюда получаем , а х находим, подставив y в любое из уравнений системы. Удобнее в 1ое в данном случае. Получаем x + 4 * 5 = 9, откуда x = -11. ответ: x = -11; y = 5.
, а х находим, подставив y в любое из уравнений системы. Удобнее в 1ое в данном случае. Получаем x + 4 * 5 = 9, откуда x = -11.
14 см и 14 см
196 см**2
Объяснение:
наибольшая площадь при одинаковом периметре будет у квадрата
56/4= 14
ок. докажем
пусть у нас есть квадрат с стороной х. его периметр - 4х, а площадь -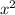
сделаем из квадрата прямоугольник того же периметра. его стороны будут (х-а) и (х+а)
периметр будет по-прежнему 4х, а площадь (х-а) * (х+а) =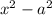
т е у любого прямоугольника того же периметра площадь будет меньше, чем у квадрата