Алгебра: Решите производные функции.

Решите производные функции.

👇

Увидеть ответ

Ответ:

olgakazakova20oy0u8c

02.01.2023

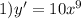
$1) y' = 10 {x}^{9}$

$2)y' = 12 {x}^{5}$

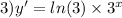
$3)y' = ln(3) \times {3}^{x}$

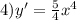
$4)y' = \frac{5}{4} {x}^{4}$

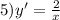
$5)y '= \frac{2}{x}$

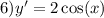
$6)y' = 2 \cos(x)$

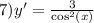
$7)y '= \frac{3}{ { \cos}^{2}(x) }$

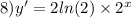
$8)y' = 2 ln(2) \times {2}^{x}$

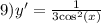
$9)y '= \frac{1}{3 { \cos}^{2} (x)}$

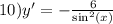
$10)y' = - \frac{6}{ { \sin}^{2} (x)}$

4,7(17 оценок)

Открыть все ответы

Ответ:

YMNIKVKOWICKAH

02.01.2023

ответ: 1) 1500 кг. 1140 кг. 2640 кг.

Объяснение:

1. 1 участок -- 25 мешков

2 участок 19 мешков --- на 360 кг меньше

25-19 = 6 мешков меньше.

В 6 мешках - 360 кг. в одном = 360/6=60 кг

с 1 участка собрали 25*60 = 1500 кг

со 2 участка собрали 19*60 = 1140 кг

с 2-х участков собрали (25+19)*60 = 2 640кг.

1500-1140 = 360 кг

***

2. Дано. Длина питомника — 857 дм,

его периметр — 2622 дм.

Чему равна площадь садового питомника?

Решение.

Р=2(a+b) = 2(857 + b);

2(857 + b) = 2622;

857+b = 1311;

b=1311-857;

b=454 дм

S=ab = 857 * 454 = ‭389 078‬ дм ².

***

3. Произведение числа 875 и суммы чисел 823 и 41 равна:

857*(823+41)=857*864= ‭740 448‬.

***

4. 609*906= 551 754.

***

5. 1 минута --- 1 руб 17 коп.

3 часа 35 минут =3*60+35=215 минут.

За 215 минут заплатит 215 * 1,17 = 251 руб 55 коп.

***

6. S=ab = 43*60 = 2580 мм² =25,8 см².

***

7. Во сколько раз миллиметр меньше метра?

1 метр = 100 см = 1 000 мм.

ответ: миллиметр меньше метра в 1 000 раз.

***

8. Переведи в метры:

40 км 80 м = 40 *1000 + 80 = 40 000+80 = 40 080 м.

4,5(47 оценок)

Ответ:

Kursova82

02.01.2023

Имеется в виду, что a, b, c - какие-то функции от x. Обычный сводящийся к рассмотрению нескольких случаев раскрытия модулей, хорош, если легко ищутся промежутки, на которых эти функции имеют определенный знак. Если же это не так, можно применить метод, который можно найти в книжке Голубева "Решение сложных и нестандартных задач по математике" (этот метод там не обосновывается, поскольку любой, берущийся за решение сложных и нестандартных задач, должен такое обоснование придумывать самостоятельно). Постараюсь это обоснование привести здесь. Основой метода служат следующие равносильности:

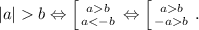
|a| $|a|b\Leftrightarrow \left [ {{ab} \atop {ab} \atop {-ab}} \right..$

Доказывать здесь их не хотелось бы. Скажем, в книжке Мерзляка, Полонского и Якира "Алгебраический тренажер" они используются без доказательства. Если эти доказательства кому-то нужны, помещайте такое задание, и я обязательно их приведу. Кстати, для тех, кто забыл, напомню, что фигурной скобкой обозначается система, а квадратной - совокупность.

Переходим к неравенству 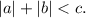|a|+|b| Перенеся |b| направо, получаем неравенство первого типа, поэтому оно равносильно системе

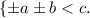
$\left \{ {{a$ Снова применяем тот же метод, теперь к каждому из неравенств системы, после чего получаем после перенесения a влево, систему из четырех неравенств, которую для экономии места и времени для написания я изображу в виде $\{\pm a\pm b$

Рассуждая аналогично, получаем, что

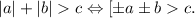$|a|+|b|c\Leftrightarrow [\pm a\pm bc.$ Естественно, здесь такое обозначение я использовал для совокупности четырех неравенств, полученных всевозможными раскрытия модулей.

Наконец, если мы имеем модуль и в правой части, то в случае неравенства |a|+|b|<|c| мы получаем систему 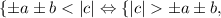$\{\pm a\pm b\pm a \pm b,$ причем каждое из этих неравенств равносильно совокупности двух уравнений, полученных разными раскрытиями модуля c.