пусть одно число х,второе у..
тогда среднее арифметическое равно (х+у)/2=7 -умножим обе часть на 2,чтобы избавиться от знаменателя
х (в квадрате) -у (в квадрате)=14
тогда получим, что
х+у=14
х (в квадрате) -у (в квадрате)=14
выразим из первого уравнения,х,и подставим во второе,и получим,
х=14-у
(14-у) в квадрате-у в квадрате=14.
раскроем скобки второго уравнения.
196+у (в квадрате)-28у-у(в квадрате)=14
приведём подобные и получим,
-28у=14-196
-28у=-182
у=6,5.
тогда,х=14-6,5=7,5.
и найдём сумму квадратов этих чисел
7,5 в квадрате+6,5 в квадрате=98,5
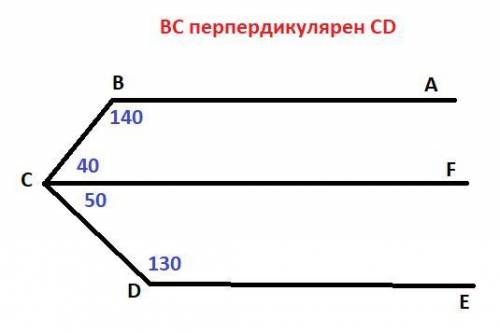
Условие: BA║DE, ∠CBA = 140°, ∠CDE = 130°. Доказать, что BC⊥CD.
Дано: BA║DE, ∠CBA = 140°, ∠CDE = 130°.
Доказать: BC⊥CD.
Доказательство:
Проведем из точки С прямую CF, параллельную прямым BA и DE.
∠CBA и ∠BCF - односторонние углы при BA║CF и секущей ВС.∠DCF и ∠CDE - односторонние углы при CF║DE и секущей CD.Сумма односторонних углов при параллельных прямых и секущей равна 180° ⇒
∠CBA + ∠BCF = 180°
∠DCF + ∠CDE = 180°
∠BCF = 180° - ∠CBA = 180° - 140° = 40°∠DCF = 180° - ∠CDE = 180° - 130° = 50°∠BCD = ∠BCF + ∠DCF = 40° + 50° = 90°
Значит, BC⊥CD, что и требовалось доказать.
смотри во влажениях. под цифрой 2 еще нужно написать что функция является ни четной ни нечетной