выпишем координаты данных векторов:
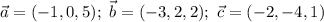
a)
координаты:
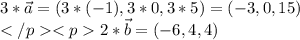
скалярное произведение векторов - число:
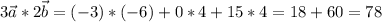
б)
координаты:
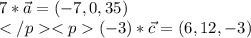
векторное произведение векторов - вектор, находим его координаты:

находим модуль(длину) полученного вектора:
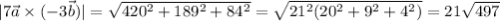
в)
координаты:
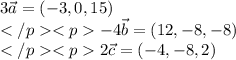
смешанное произведение векторов - число, находим его:
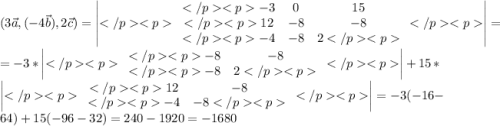
г)
Координаты:
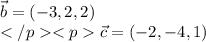
Векторы коллинеарны, если их соответствующие кординаты пропорциональны
Проверим это утверждение:
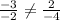
Данное равенство неверно, значит векторы b и c не коллинеарны
Векторы ортогональны, если их скалярное произведение равно нулю.
Проверим это утверждение:
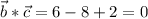
- верно, значит данные векторы ортогональны
Векторы b и c ортогональны
д)
Координаты:
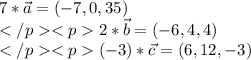
Три вектора компланарны, если их смешанное произведение равно нулю.
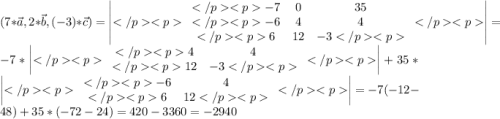
-2940 не равно нулю => данные векторы не компланарны.
Объяснение:
Найдём производную нашей данной функции: f(x) = (3x^2 - 2) / x^3.
Воспользовавшись основными формулами и правилами дифференцирования:
(x^n)’ = n * x^(n-1).
(с)’ = 0, где с – const.
(с * u)’ = с * u’, где с – const.
(u ± v)’ = u’ ± v’.
(u / v)’ = (u’v - uv’) / v2.
y = f(g(x)), y’ = f’u(u) * g’x(x), где u = g(x).
Таким образом, производная нашей данной функции будет следующая:
f(x)' = ((3x^2 - 2) / x^3)’ = ((3x^2 - 2)’ * x^3 - (3x^2 - 2) * (x^3)’) / (x^3)^2 = (((3x^2)’ - (2)’) * x^3 - (3x^2 - 2) * (x^3)’) / x^6 = ((3 * 2 * x - 0) * x^3 - (3x^2 - 2) * (3 * x^2)) / x^6 = (6x^3 – 9x^4 -6x^2) / x^6 = ((x^2) * (6x – 9x^2 -6)) / x^6 = (6x – 9x^2 -6)) / x^4.
ответ: Производная нашей данной функции будет равна f(x)' = (6x – 9x^2 -6)) / x^4.
ответ: ±1, ±7