
ответ:(5;0);(-5;0)
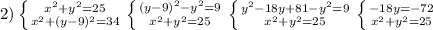
ответ:(-3;4)(3;4)
Объяснение:
Разложить число на простые множители значит записать число как произведение простых чисел .
Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей Например, числа 2,3,5,7, – простые, а числа 6(2*3),8(2*4),9(3*3) – составные.
Число 388 , оканчивается на 8 значит делится на 2
388:2=194, оканчивается на четное , значит также делится на 2
194 :2= 97 ,вспомним признаки делимости на 3 и 9 , число делится если сумма его цифр делится на 3 или 9.На четыре делится если 2 его последние цифры нули или образуют число которое делится на 4, На пять делится если число оканчивается на 5 или 0.осталось число 6 и 8. На 6 делится если одновременно делится на 2 и 3 , и число делится на 8, если три его последние цифры - нули или образуют число, которое делится на 8.
97=9+7=16, ни на одно число не делится, кроме 1 и самого себя значит 97 это простое число.
388=2*2*97
Число 2520
2520:2= 1260 ( признак делимости на 2)
1260:2=630 ( признак делимости на 2)
630:2=315 ( признак делимости на 5)
315:5=63 ( признак делимости на 3 и 9; 6+3=9 делится и на 3 и на 9
63:3=21 (2+1=3, признак делимости на 3 )
21:3=7 ( неделимое, простое число)
2520 = 2*2*2*3*3*5*7
2) Чтобы обратить обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
3 2/5=17/5=17:5=3,4 мы получили конечную десятичную дробь, поскольку в знаменателе обыкновенной дроби стоит 5 ( получить конечную десятичную дробь можно если знаменатель обыкновенной дроби содержит простые множители 2 и 5)
43/30=43:30=1,4 33333… = 1,4(3), поскольку знаменатель обыкновенной дроби содержит кроме 2 и 5 еще 3, то она не может быть представлена конечной десятичной дробью.
Для вычисления пары чисел которые будут решением этого уравнения мы применим один из решения системы уравнений:
5x - 3y = 0;
3y + 4x = 27.
Осмотрев оба уравнения системы мы лицезреем, что перед переменной y стоят в обеих уравнениях обоюдно противоположные коэффициенты.
Сложим почленно два уравнения системы и получим:
5x + 4x = 0 + 27;
y = (27 - 4x)/3.
Так же из второго уравнения мы выразили переменную y через x.
Решаем 1-ое уравнение системы:
9x = 27;
x = 27 : 9;
x = 3.
Система уравнений:
x = 3;
y = (27 - 4 * 3)/3 = (27 - 12)/3 = 15/3 = 5.
Объяснение:
1) x^2-y^2=25,
x^2+y^2=25; получается система уравнений, перед знаком системы ставим знак "+", тогда " -y^2 и +y^2" сократятся, останется
2x^2=50
x^2=25
x= +5, x=-5
2) x^2+y^2=25
x^2+(y-9)^2, теперь перед знаком системы ставим знак "-", тогда X^2 исчезает останется
y^2-(y-9)^2=-9
y^2- y^2+18y-81=-9
18y=72
y=4
3) x^2+xy+x=10
y^2+xy+y=36, а вот третье не знаю щас еще подумаю.