В решении.
Объяснение:
Постройте графики функций y= -3/x и y=x+4 Укажите координаты точек пересечения этих графиков.
График y= -3/x гипербола. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -5 -4 -3 -2 -1,5 -1 -0,5 1 1,5 2 3 4 5
у 0,6 0,75 1 1,5 2 3 6 -3 -2 -1,5 -1 -0,75 -0,6
y=x+4. Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 3 4 5
Координаты точек пересечения гиперболы и прямой (-1; 3) (-3; 1).
Точки пересечения находятся во второй четверти.
1) x∈(1;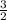
)
2) x∈(-∞; -3)∪(1; +∞)
Объяснение первого неравенства:
Чтобы произведение было меньше нуля, множители должны иметь разные знаки. Тогда получаем две системы (знака системы сайт не имеет, строчки должны быть объединены фигурной скобкой).
Первая:
x-1<0
2x-3>0
Вторая:
x-1>0
2x-3<0
Решение первой:
x-1<0
x<1;
2x-3>0
2x>3
x>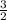
;
Поскольку мы решали систему, нужно найти пересечение решений. Здесь пересечение - пустое множество, потому что 3/2 больше 1.
Решение второй:
x-1>0
x>1;
2x-3<0
2x<3
x<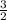
Пересечение решений - x∈(1;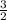
) (скобки ставим круглые, потому что знак неравенства строгий)
Объяснение второго неравенства:
Чтобы произведение было больше нуля, множители должны иметь один знак. Тогда получаем две системы:
Первая:
x+3>0
x-1>0
Вторая:
x+3<0
x-1<0
Решение первой:
x+3>0
x>-3;
x-1>0
x>1;
Пересечение: x∈(1; +∞)
Решение второй:
x+3<0
x<-3;
x-1<0
x<1;
Пересечение: x∈(-∞; -3)
Пересекаем решения первой и второй систем и получаем: x∈(-∞; -3)∪(1; +∞)