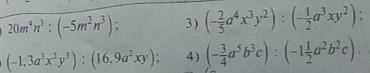
В решении.
Объяснение:
1) Решить неравенство:
(x+4)²-x² < 10x-1
х² + 8х + 16 - х² < 10x - 1
8x - 10x < -1 - 16
-2x < - 17
x > -17/-2 (знак неравенства меняется при делении на минус)
x > 8,5
Решение неравенства: х∈(8,5; + ∞).
Неравенство строгое, скобки круглые.
2) Решите задачу с составления уравнения. Разность двух чисел равна 9, а разность их квадратов 369. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 9
х² - у² = 369
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 9 + у
(9 + у)² - у² = 369
81 + 18у + у² - у² = 369
18у = 369 - 81
18у = 288
у = 288/18
у = 16 - второе число.
х = 9 + у
х = 9 + 16
х = 25 - первое число.
Проверка:
25 - 16 = 9, верно.
25² - 16² = 625 - 256 = 369, верно.
-6=-9(7+x)+4x
-6=-42-9х+4х
-6=-42-5х
5х=-36
х=-7,2
ответ. х=-7,
2-х+4(7-х)=-7х+5 -х+28-4х = -7х+5
-х-4х+7х = 5-282х=-23
х=-23/2
х=-11,5
-5x - x + 5(x-5) = -(-5-x)-4
-5x - x + 5x - 25 = 5x + x - 4
-7x = -4 + 25
-7x = 21
x = -3
Как то так))