Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4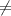 
0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2
где A, B, C - это константы, (A и B одновременно не равны нулю)
Это общее уравнение прямой на координатной плоскости XOY.
Показать (или доказать) это можно разными
Так вот: 6x+3y+18 = 0, это уравнение прямой. Чтобы построить эту прямую на координатной плоскости достаточно найти две различные точки, принадлежащие этой прямой. Найдем какие-либо две точки (два частных решения этого уравнения. Например: положим x_1=0, подставим это в уравнение, получим 3y+18 = 0, <=> y = -18/3 = -6.
Первая точка это x_1=0, и y_1=-6.
Аналогично находим вторую точку прямой: положим y_2=0, подставим это значение в уравнение прямой, получим 6x+18=0, <=> x=-18/6 = -3.
Вторая точка у нас имеет координаты x_2=-3 и y_2 = 0.
Теперь следует отметить эти точки на координатной плоскости XOY (на графике), затем взять линейку и с ручки или карандаша провести через эти точки прямую линию. Это и будет график данной в условии прямой.