Вариант 2. 1. Составьте одну из возможных формул n-го члена последовательности по первым пяти ее
членам: 1, 3
1
; 5
1
; 7
1
; 9
1
….
[1]
2. В арифметической прогрессии первый член 10 и разность d .
a) Найдите пятый член прогрессии и сумму первых пяти членов прогрессии.
[3]
b) Обозначим n-й член прогрессии через an. Найдите наименьшее натуральное число n
такое, что an >170.
[3]
3. Сумма трех чисел, представляющих возрастающую арифметическую прогрессию равна 21. Если к
ним, соответственно, добавить 2, 3, и 9 то образованные числа составят геометрическую прогрессию.
Найти наибольшее из искомых членов прогрессии.
[4]
4. Первый, второй и третий члены геометрической прогрессии соответственно равны
2k 8; k; k , где k - положительное число.
а) Найдите значение k .
b) Найдите сумму бесконечно убывающей геометрической прогрессии.
[4]
5. Работники получили задание выкопать колодец. За первый выкопанный в глубину метр колодца
им платят 2000 тг, а за каждый следующий – на 2000 тг больше, чем за предыдущий. Сколько денег
заплатят работникам за выкопанный колодец глубиной 12 м
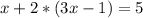
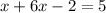
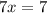
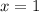
Дано:
|y=3x-1
|x+2y=5
Решение
Подставим первое уравнение во второе:
Подставляем полученное значение в первое уравнение:
y=3x-1, при x=1
y=3-1
y=2
ответ: (1;2)
2.
Дано
|x+5y=13
|3x-y=-9
Решение
Выразим из первого уравнения переменную x:
x=13-5y
Подставим полученное выражение во второе уравнение:
3*(13-5y)-y=-9
Раскроем скобки:
39-15y-y=-9
Перенесем неизвестное значение в левую часть, а константы в правую:
-16y=-9-39
y=(-48)/(-16)
y=3
Подставим полученное значение в первое преобразованное уравнение:
x=13-5y, при y=3
x=13-5*3
x=13-15
x=-2
ответ: (-2;3)