50 и 40 км/ч
Объяснение:
Составим таблицу:
Мотоциклисты | Скорость | Время | Расстояние
Первый | х км/ч | 200/х ч | 200 км
Второй | х-10 км/ч | 200/(х-10) | 200 км
Пусть х км/ч - скорость первого мотоциклиста, тогда скорость второго Х-10 км/ч. Время, затраченное одним мотоциклистом на путь из пункта А в В считается по формуле время = расстояние/скорость. Так как расстояние между населенными пунктами = 200 км, время, затраченное первым мотоциклистом = 200/х часов, а вторым = 200/(х-10) часов.
Зная, что второй мотоциклист потратил в пути на один час больше, составляем уравнение:
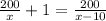
В уравнении мы прибавляем час к времени первого мотоциклиста, так как он приехал на час быстрее. И чтобы уравнять времена, затраченные первым и вторым мотоциклистом, к быстрому товарищу нужно добавить время опоздания второго.
О.Д.З. х ≠10, х≠0, х>0 (так как скорость не может быть отрицательной, а равной нулю она быть не может по другим условиям ОДЗ)
Решим уравнение:
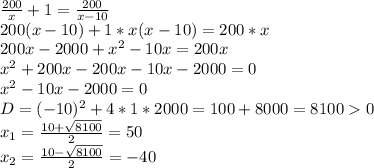
Корень х2 = -40 не удовлетворяет ОДЗ
Значит, скорость первого мотоциклиста = 50 км/ч
Тогда скорость второго = 50-10 = 40 км/ч
√(x² -2x+1) -2√(4 -4x+x²+8x) < x ;
√(x-1)² -2√(x +2)² < x ;
|x-1| -2|x+2| < x ;
2|x+2| -|x-1| +x > 0 ;
(-2) 1
а)
x < -2 .
---
-2(x+2) +(x-1) +x >0 ⇒ -5 > 0 (неверное числовое неравенство)
В интервале (-∞ ; -2) нет решения)
б)
-2 ≤ x < 1 .
---
2(x+2) +(x-1) +x >0 ;
4x > - 3;
x > -3/4. * * * -3/4< x < 1 * * *
в)
x ≥ 1 .
---
2(x+2) -(x-1) +x > 0 ;
2x > -5 ;
x > -5/2 * * * x ≥ 1 * * *
общее решения неравенства : x ∈( -3/4 ; ∞) .
ответ : наименьшее целое решение неравенства будет x =0.