Решение системы уравнений (5; 8)
Объяснение:
Решить систему уравнений методом сложения:
(х+3)/2 - (у-2)/3 =2
(х-1)/4 + (у+1)/3 =4
Умножить первое уравнение на 6, второе на 12, чтобы избавиться от дроби:
3(х+3)-2(у-2)=12
3(х-1)+4(у+1)=48
Раскрыть скобки:
3х+9-2у+4=12
3х-3+4у+4=48
Привести подобные члены:
3х-2у= -1
3х+4у=47
Умножить первое уравнение на -1, чтобы применить метод сложения:
-3х+2у=1
3х+4у=47
Складываем уравнения:
-3х+3х+2у+4у=1+47
6у=48
у=8
Теперь подставляем значение у в любое из двух уравнений системы и вычисляем х:
3х-2у= -1
3х= -1+2у
3х= -1+2*8
3х=15
х=5
Решение системы уравнений (5; 8)
внутренние 135° 150° 156°
внешние 45° 30° 24°
Объяснение:
Если n-угольник правильный, то все его углы равны между собой. Сумма всех внутренних углов n-угольника вычисляется по следующей формуле
S=180°(n-2), где n- количество углов, тогда один угол, будет равен отношению суммы всех углов к количеству, т.е. ∠=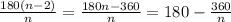
. подставим вместо n искомые числа
n=8,∠=135°
n=12,∠=150°
n=15,∠=156°
Внешние углы, это углы, образующие с внутренним углом угол 180 градусов, а значит нужно вычесть от 180 величину внутреннего угла, т.е.
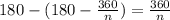
тогда
n=8,∠=45°
n=12,∠=30°
n=15,∠=24°
у=-3х+1
Составить уравнение прямой.
Объяснение:
Уравнение заданной прямой:
у=-3х-4
==>
k=-3
Уравнение линейной функции:
у=kx+b
k - угловой коэффициент;
b - cвободный член.
Условие параллельности пря
мых:
прямые параллельны, если
равны их угловые коэффици
енты.
==>
у искомой прямой k=-3.
Искомая прямая проходит че
рез точку (2;-5)
==>
координаты этой точки х=2 и
у=-5 удовлетворяют урав. ис
комой прямой.
Подставляем уже известный
угловой коэффициент и задан
ные координаты точки в урав
нение прямой:
k=-3
y=-5
x=2
-5=-3×2+b
b=-5+6
b=1
Все компоненты известны
(k=-3; b=1). Составим урав
нение:
y=-3x+1
Это уравнение искомой прямой.
у=-3х+1