Обозначим через аi число очков, выбитых первым стрелком при i-м выстреле, а через bi число очков, выбитых вторым стрелком при i-м выстреле.
Тогда из условий задачи следует:
а1+а2+а3= b1+b2+b3, (1)
а3+а4+а5= 3(b3+b4+b5), (2)
Из приведенных попаданий заключаем, что равенство (2) может выполняться, если b1, b2, b3, минимальные по числу очков попадания, а а3, а4, а5 максимальные и сумма а3+а4+а5 кратна трем. Отсюда видно, что b3, b4, b5, это числа 2, 3 и 4, а а3, а4, а5 это числа 10, 9, 8. Далее видим, что первыми четырьмя выстрелами (каждый стрелок сделал по два) они выбили очки: 9, 8, 5, 4. Используем условие (1). Очевидно, что при этом сумма а1+а2 должна быть наименьшей при ее выборе из четырех чисел (9, 8, 5, 4), а b1+b2 наибольший при выборе ее из тех же чисел. Это возможно при a=5, a2=4, a3=10, b1=9, b2=8, b3=2.
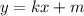: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 
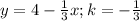. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 
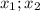, два произвольных числа, но 
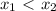. Пусть мы имеем функцию 
, тогда вычисляем значения функции в этих двух точках, имеем 
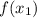и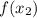 
, так вот, если 
, тогда функция возрастающая, если же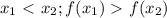 
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
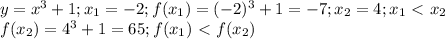, т.е. функция возрастающая. А вот задание с 
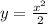не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 
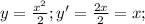. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 
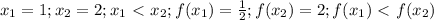, функция возрастает, что и требовалось доказать.
1. Функция касательной имеет вид Y=f(Хо) + f'(Хо) (Х-Хо)
В нашем случае это: Y=ln(Хо/2) + 1/Хо*(Х-Хо)
2. Т. к. эта прямая должна проходить через начало координат, то подставляем Х=0 и Y=0:
ln(Хо/2) + 1/Хо*(0-Хо) =0
ln(Хо/2) - 1=0
ln(Хо/2) = 1
Хо/2 = e
Хо=2e
3. Теперь в функцию касательной подставляем Хо:
Y=ln(2e/2) + (1/2e)(X-2e)
Y=1 + X/2e - 1
Окончательный вид: Y=X/2e