Мы имеем график функции y = x3 и точки: (3; -27),Для того, что бы определить лежат ли они на заданном графике, подставим их в функцию.
1 ) (3; -27). х = 3, у = -27.
y = 33 = 27.
Вывод : данная точка не принадлежит графику, заданного функцией y = x3
а) две точки пересечения (два корня)
b)
Объяснение:
a) 
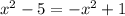 в)
в)  окружность R=3, O(0;0) и
окружность R=3, O(0;0) и

 парабола с ветвями вниз, вершина(0;4)
парабола с ветвями вниз, вершина(0;4)
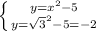 четыре точки симметричные относительно
четыре точки симметричные относительно
 оси "y"
оси "y"
б) xy=3 или 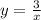 гипербола, точка симметрии (0;0)
гипербола, точка симметрии (0;0)
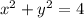 окружность R=2 центр (0,0)
окружность R=2 центр (0,0)
точек пересечения графиков нет, самые близкие точки к началу кординат в точках х=у, у гиперболы 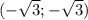 и
и 
у окружности  и
и 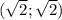
г)  это две окружности: одна R=4, центр (0;0)
это две окружности: одна R=4, центр (0;0)
другая R=2 центр (0;2), точка касания (0;4) одна.
ну а графики придется рисовать по клеткам, используя циркуль и лекала для точности построения. Удачи.