1. Найдите значение выражения:
¼ х^3 + 3у^2 при х = -2 и у = -1
0,25*(-2)^3+3*(-1)^2= -2 + 3 = 1
2.Решите систему уравнений:
х + 2у = 11 /(-5)
5х – 3у = 3
Метод алгебраического сложения
-5x-10y=-55
5х – 3у = 3
=============
-10y-3y=-55+3
-13y=-52
y=4
Найдём x:
x=11-2y=11-2*4=11-8=3
ОТВЕТ: (3; 4)
3. Задача
Пусть планируемая скорость велосипедиста равна х км/ч, тогда действительная скорость равна х+3 км/ч.
Велосипедист должен был проехать весь путь за 2 часа, т.е. расстояние составляет 2х км.
Известно, что велосипедист на весь путь затратил 1 и две третьих часа (или 5/3 часа.
Составим уравнение:
2х=5/3(х+3)
2х=5/3х+5
2х-5/3х=5
1/3х=5
х=5:1/3
х=15(км/ч)-планируемая скорость
Путь равен 2*15=30 (км)
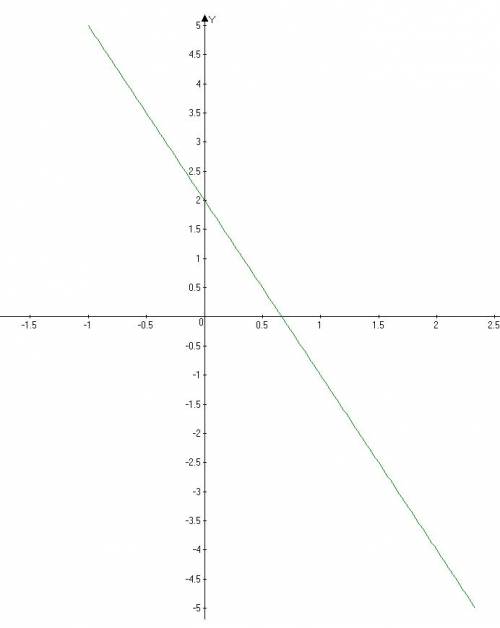
4. а) график функции
у = 2 – 3х
см. рис
б) Принадлежит ли графику функции точка М (9; -25)?
Да, принадлежит.
ответ: Нет.
Из условия следует, что f(x) = (x – a)(x – b), где a ≠ b.
Пусть искомый многочлен f(x) существует.
Тогда, очевидно f(f(x)) = (x – t1)²(x – t2)(x – t3).
Заметим, что t1, t2, t3 — корни уравнений f(x) = a и f(x) = b, при этом корни этих уравнений не совпадают, поэтому можно считать, что уравнение f(x) = a имеет один корень x = t1.
Рассмотрим уравнение f(f(f(x))) = 0. Его решения, очевидно, являются решениями уравнений f(f(x)) = a и f(f(x)) = b. Но уравнение f(f(x)) = a равносильно уравнению f(x) = t1 и имеет не более двух корней, а уравнение f(f(x)) = b — не более четырех корней (как уравнение четвертой степени).
То есть уравнение f(f(f(x))) = 0 имеет не более 6 корней.