Так как при вращении на 360°=2П радиан , мы попадаем в ту же точку ,
то угол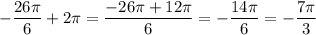 
попадает в ту же
точку на единичной окружности , что и угол (-26П/6) .
Но угол (-7П/3) не лежит между 0 и 2П . Поэтому надо прибавить не 2П,
а больше , чтобы попасть в промежуток [ 0 ; 2П ] . Подбираем число n .
Если прибавить 3*2П , то получим
![-\dfrac{26\pi }{6}+3\cdot 2\pi =\dfrac{-26\pi +36\pi }{6}=\dfrac{10\pi }{6}=\dfrac{5\pi }{3}=300^\circ\ \ ,\ \ \ \ \dfrac{5\pi }{3}\in [\ 0\ ;\ 2\pi \ ]](/tpl/images/4595/4137/96e22.png)
Полученный угол принадлежит промежутку [ 0; 2П ] .
Замечание. Если прибавить 2*2П , то не получим угол из
промежутка [ 0;2П ] . Действительно,
.
То есть можно сообразить, что в числитель к (-26П) надо прибавить число, большее 26П, чтобы получить положительный угол. И соответственно подбирать n .
Если прибавить 4*2П , то получим угол, который больше, чем 2П. Действительно,
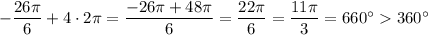
То есть n=2 и n=4 не подходит , а n=3 как раз подходит .
Объяснение:
Решение квадратного неравенства
Неравенство вида
где x - переменная, a, b, c - числа, , называется квадратным.
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения . Для этого необходимо найти дискриминант данного квадратного уравнения. Можно получить 3 случая: 1) D=0, квадратное уравнение имеет один корень; 2) D>0 квадратное уравнение имеет два корня; 3) D<0 квадратное уравнение не имеет корней.
В зависимости от полученных корней и знака коэффициента a возможно одно из шести расположений графика функции
Если требуется найти числовой промежуток, на котором квадратный трехчлен больше нуля, то это числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если требуется найти числовой промежуток, на котором квадратный трехчлен меньше нуля, то это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое - не входят.
Такой метод решения квадратного неравенства называется графическим.