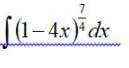
![\int\limits {(1 - 4x)}^{ \frac{7}{4} } dx = - \frac{1}{4} \int\limits {(1 - 4x)}^{ \frac{7}{4} } d( - 4x) = \\ = - \frac{1}{4} \int\limits {(1 - 4x)}^{ \frac{7}{4} } d(1 - 4x) = \\ = - \frac{1}{4} \times \frac{ {(1 - 4x)}^{2} }{ \frac{11}{4} } + C = - \frac{1}{11} \sqrt[4]{ {(1 - 4x)}^{11} } + C](/tpl/images/1607/4034/51b89.png)
1) функция принимает мах (или мин) значение либо на концах отрезка, либо в точках, где производная равна 0.
f(2)=6-2=4
f(3)=6-3=3
f `(x)=-1 не равно 0, выбираем из 2-х точек наиб (или наим) - это мах=4, мин=3
или f `(x)=4x-6, 4x-6=0, 4x=6,x=1,5
f(1,5)=2* (1,5^2)-6*1,5+2=6,5
f(2)=2* 2^2 - 6*2 +2=-2
f(3)=2* 3^2 - 6*3+2=2
выбираем из значений 6,5 -2 2 - наиб=6,5 наим=-2
2) Для нахождения экстремума найти производную и приравнять ее к нулю:
y `=3x^2, 3x^2=0, x=0
+ +
0x
здесь производная при переходе через точку 0 не меняет знак, следовательно, 0 не является экстремумом, а просто стационарная точка. А если при переходе через точку производная меняет знак с + на - ,то получаем точку мах; с - на + -точка мин