Пусть скорость горной реки х
Плот плывет по реке 21 км в течение 21:х часов
Туристы на лодке все расстояние проплыли за такое же время:
54:(12+х) плыла лодка по реке + 6:12 по озеру и все это равно времени, за которое плот плывет по реке 21 км, =21:х
Составим и решим уравнение:
54:(12+х) +0,5 =21:х
Умножим обе части на х(12+х), чтобы избавиться от дробей:
54х +0,5х(12+х) =21(12+х)
54х +6х +0,5х² =252+21х
0,5х²+39х -252=0
D=b²-4ac=39²-4·0.5·-252=2025
Так как дискриминант больше нуля, то уравнение имеет два корня
Один отрицательный и не подходит ( -84)
Второй = 6
Скорость течения горной реки 6 км/ч
Объяснение:
из всех правил сдвига графика функций, я выберу те, которые касаются нашей функции
1. если ФУНКЦИЯ умножается на число 0<m<1 , то происходит сжатие её графика вдоль оси oy в 1/m раз
2. если АРГУМЕНТ функции умножается на 0<k<1, то график функции растягивается от оси оу в 1/k раз
3. если к АРГУМЕНТУ функции добавляется константа b y(x+b), то происходит сдвиг (параллельный перенос) графика вдоль оси оx на b единиц влево .
теперь проделаем все это с нашей функцией
начнем с простого
1. у нас ФУНКЦИЯ умножается на число 0< 1/4 <1, значит мы будем сжимать функцию y = cos(x) в 4 раза вдоль оси оу
2. у нас АРГУМЕНТ функции умножается на 0< 1/2 <1, значит мы будем растягивать график у = cos(x) от оси оу в 2 раза
3. а вот теперь тут будет не так просто. поскольку правило 3 справедливо для графика функции y(x+b), нам надо привести свою заданную функцию к такому виду
таким образом у нас будет сдвиг (параллельный перенос) графика
у = cos(x) вдоль оси оx на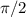 
единиц влево
ну и вот что должно получиться.
Объяснение:
х^2 − 8х + с = 0.
х₁ ₂ = (8±√(64-4с)) /2
0∠64-4с есть 2 разных корня. 4с∠64 при с∠16 х₁ ≠ х₂
a) При каких значениях параметра с данное уравнение имеет два одинаковых действительных корня?
При равенстве 0 дискриминанта имеется два одинаковых корня.
0=64-4с 4с=64 с=16
х₁ ₂ = (8±√(64-4*16)) /2
х₁ ₂ = (8±√(64-64)) /2
b) Найдите эти корни уравнения.
х₁ = (8-0) /2 = 4
х₂ = (8+0) /2 =4