![a_1=2\ \ \ \ \ \ \ \ \ \ \ q0 \\ \\ a_1*a_2*a_3*a_4=1024 \\ \\ a_1*a_1q*a_1q^2*a_1q^3=1024 \\ \\ a_1^4*q^6=1024 \\ \\ 2^4q^6=1024 \\ \\ 16q^6=1024 \\ \\ q^6=64 \\ \\ \left \{ {{q^6=64} \atop {q0}} \right \\ \\ q=\sqrt[6]{64}=2](/tpl/images/0160/9141/2c66e.png)
ответ: 2
Решение начнем с того, что перенесем все члены уравнения в одну сторону:
sin^2 (3x) = cos^2 (3x) – 1
cos^2 (3x) – sin^2 (3x) – 1 = 0.
Обратим внимание на разницу первых двух членов. Эту разницу можно свернуть в более короткую и удобную форму по формуле косинуса двойного угла, которая записывается следующим образом:
cos (2x) = cos^2 (x) – sin^2 (x).
В качестве аргумента в нашем случае выступает аргумент 3х. Запишем уравнение, свернув разницу первых двух членов по выше упомянутой формуле:
cos (2 * 3x) – 1 = 0
cos (6x) – 1 = 0.
Перепишем полученное уравнение в более удобной форме:
cos (6x) = 1.
Решим полученное тригонометрической уравнение любым из доступных Если косинус от любого аргумента равен единице, то аргумент этой функции равен 2 * пи * n. В данном случае аргумент косинуса равен 6х:
6x = 2 * пи * n.
Осталось вычислить значение переменной х. для этого разделим обе части уравнения на 6:
x = (пи * n ) / 3
x = пи / 3 * n.
ответ. x = пи / 3 * n, n – любое целое число.
Проводим две перпендикулярные хорды
АВ и DC
точку пересечения этих хорд обозначим буквой Е
AE/EB=4/6,CE/ED=4/6
из центра окружности, т.е. из точки О проведем перпендикуляры к хорде AB и к хорде DC, эти перпендикуляры делят наши хорды пополам.
Перпендикуляр опущенный в DC назовем M1, а опущенный в AB назовем M2
таким образом, СМ1 - это половина СD, т.е. СМ1=5, потому что вся СD=10
из этого следует что ЕМ1=СМ1-СE=1, следовательно EM2=1
поскольку EM1OM2 - прямоугольник, то все его стороны равны, следовательно ОМ1=ОМ2=1
ответ: 1
Пусть q - знаменатель геометрической прогрессии.
Формула n-ого члена: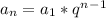
Выражаем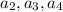 :
:
ответ: q=2