ответ: на 25%.
Объяснение:
обозначим размеры прямоугольника х и у; пусть х<у;
периметр прямоугольника 2(х+у)
тогда длина стороны отрезанного квадрата (х); периметр оставшейся части прямоугольника 2(х+у-х) = 2у
2у составляют 80% от 2(х+у)
2у = 0.8*2(х+у)
у = 0.8х + 0.8у
0.2у = 0.8х
у = 4х
первоначальная площадь прямоугольника х*у = х*4х = 4х^2
площадь оставшейся части
х*(у-х) = х*(4х-х) = х*3х = 3х^2
4х^2 100%
3х^2 ? %
?% = 3х^2*100 / (4х^2) = 300 / 4 = 75%, следовательно, площадь уменьшилась на 100% - 75% = 25%
Тогда получим систему уравнений: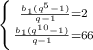
Разделим второе уравнение на первое:
q=2.
ответ: 2.