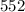
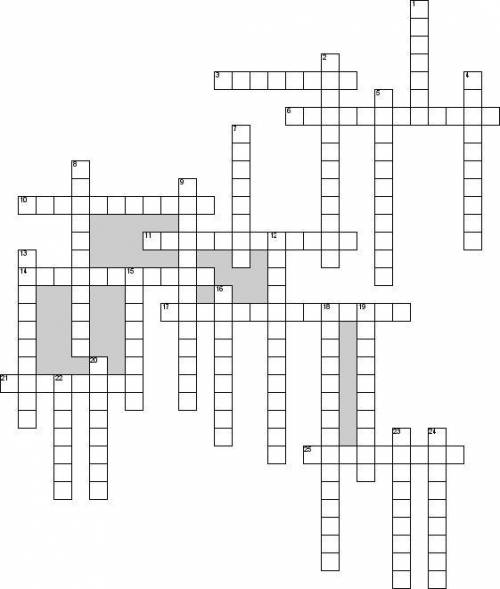
3. Функция, меняющая знак при изменении знака независимого переменного, называется
6. Как располагаются графики линейных функций, если угловые коэффициенты различны
10. Если функция непрерывна во всех точках своей области определения, то она называется
11. Плоскость, на которой выбрана система координат
14. Множество, на котором задаётся функция, называется областью
17. О.О показательной функции множество R всех … чисел
21. График квадратичной функции
25. Как называется функция вида y=k/x
По вертикали
1. Один из задания функции
2. Если на промежутке большему значению аргумента соответствует большее значение функции, то функция …
4. Точки минимума и максимума называют точками
5. Как располагаются графики линейных функций, если угловые коэффициенты различны
7. Множество всех значений функции, которые она принимает при переборе всех x из области определения
8. Как расположены графики функций y=kx и y= kx+b
9. График прямой пропорциональности расположен в первой и третьей четвертях(квадрантах), если значение k …
12. Каким задана функция y = f (x)
13. Пара чисел, определяющая положение точки на координатной плоскости
15. Как называется функция y= kx+b
16. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется
18. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется
19. Периодом функции назывется число
20. Как называется функция вида y=x2?
22. Координатную прямую x называют ось …
23. Как называется функция в некотором промежутке, если большему значению аргумента этого промежутка соответствует меньшее значение функции
24. Функциональная зависимость выражается словами, то это какой задания функции
1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
ответ: a = - 4, b = - 5 или a = 5, b = 4.