1. Найдите значение коэффициента k, если известно, что график функции у= Проходит через точку с координатами А ( -4; –2).
A) 2
B) 8
C) -8
D) -2
3. Задайте формулой функцию, график которой проходит через точку (0;-5) и параллелен графику функции y = 6x.
4. Решите графическим методом систему уравнений:
5. Найдите:
a) область определения функции, заданной формулой:
1) у = 6х -2; 2) у = ;
b) область значений функции у = , на отрезке -1
6 . Имеются данные о количестве дежурств 15 сотрудников кафедры за месяц
3 ,0, 5, 7 ,4 ,3, 1, 9 ,5, 3 ,4, 4, 2 ,8, 5
a) постройте таблицу абсолютных частот и таблицу относительных частот;
b) укажите самое распространенное количество дежурств;
c) проверьте таблицу относительных частот на непротиворечивость
.
7. График функции заданной уравнением у = (а+1) х +а - 6 пересекает ось абсцисс в точке с координатами (2;0).
а) найдите значение а;
в) запишите функцию в виде y=kx + b
с) не выполняя построения графика функции, определите через какую четверть график не проходит
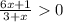
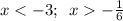
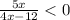
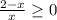
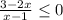
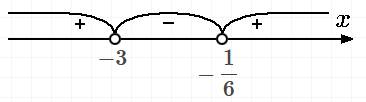



Решим линейное уравнение 6x+1=0
Корень уравнения: x=−1/6
теперь линейное уравнение x+3=0
Корень уравнения: x=−3
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале. (см. приложение)
ответ: x∈(−∞;−3)∪(−16;+∞)
или
2)
Корни уравнения 5x=0
x1=0
линейное уравнение x−12=0
Корень уравнения: x=12
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
ответ: x∈(0;12) или 0<x<12
3)
линейное уравнение −x+2=0
Корень уравнения: x=2
линейное уравнение x=0
Корень линейного уравнения: x=0
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
ответ: x∈(0;2] или 0<x≤2
4)
Решим линейное уравнение −2x+3=0
Корень уравнения: x=1,5
Решим линейное уравнение x−1=0
Корень уравнения: x=1
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
ответ: x∈(−∞;1)∪[1,5;+∞) или x<1;x≥1,5