
![A_1(7;7;8)\ ,\ A_2(6;6;8)\ ,\ A_3(8;5;8)\ ,\ A_4(8;1;1)\\\\\\1)\ \ \overline{A_1A_2}=(-1;-1;0)\\\\|\overline{A_1A_2}|=\sqrt{(-1)^2+(-1)^2+0^2}=\sqrt2\\\\\\2)\ \ A_1A_2:\ \ \dfrac{x-7}{-1}=\dfrac{y-7}{-1}=\dfrac{z-8}{[0]}\ \ \ ili\ \ \ \ \left\{\begin{array}{l}x=7-t\\y=7-t\\z=8\end{array}\right](/tpl/images/1614/7227/cb564.png)
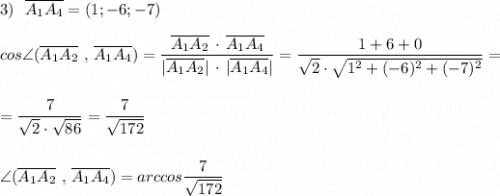
Решение
KLMN - ромб (все стороны равны).
Площадь ромба равна половине произведения диагоналей,
диагонали ромба - равны сторонам прямоугольника,
поэтому площадь ромба равна половине площади прямоугольника.
Ромб разделен на три треугольника MNP, NKP и MPL.
Площадь треугольника MNP равна сумме площадей NKP и MPL,
так как основание треугольника MNP - MN, равно сумме оснований NKP и MPL - KP и PL, а высоты, проведенные к этим основаниям равны . Значит, площадь треугольника MNP равна половине площади ромба KLMN и четверти площади прямоугольника ABCD.
Площадь треугольника MNP = 36/4 = 9.
ответ: 9

ОДЗ: 

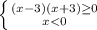
+ - +
////////////////////////-3_________________3/////////////////////////////////////
x∈ (-∞; -3]∪[3; +∞)
- +
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\0__________________________
x∈(-∞; 0)
Общее решение:  иначе x∈(-∞; -3]
иначе x∈(-∞; -3]
ответ: x∈(-∞; -3]