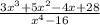
-------------------------

равнение энштейна для красной границы фотоэффекта равно : hv=aв;
hc/lmax=aв
hc/l=hc/lmax+mu^2/2, откуда
l=2hc/(hc/lmax)+mu^2=2*6,62*10^(-34)*3*10^8/(6,62*10^(-34)*3*10^8/6,9*10^(-7))+9*10^(-31)*4*10^12 = 39,72*10^(-26)/2,9*10^(-19)+36*10^(-19) = 10^(-7)м
u=2000км/с =2*10^6м/с
lmax=690нм=6,9*10^(-7)м
h=6,62*10^(-34)дж*с
m=9*10^(-31)кг
ответ разместил: Гость
нам надо узнать сколько в сутках всего секунд
значит 24 часа составляют 1440 минут или 86400 секунд(24*60*60=86400)
теперь пропорция 86400===86.4
1 х
найдем х
86400*х=1*86.4
х=86.4/86400=0.001 см
ответ 0.001см
.
Объяснение:
0
Перенумеруем все города. Для городов i, j направим дорогу из города с меньшим номером в город с большим номером. Тогда при проезде по дорогам мы всегда приезжаем в города с большими номерами, и обратно не возвращаемся.
Из города 1 можно добраться до всех, а из n нельзя выехать. Единственный путь, проходящий все города -- это 1-2-...-n.
Теперь надо показать, что такая конструкция всего одна с точностью до перенумерации городов. Из этого будет следовать, что её осуществить ровно n!.
Для начала можно доказать, что имеется город, из которого нельзя выехать. В противном случае мы можем бесконечно долго путешествовать, и какие-то посещаемые города при этом повторятся. Это значит, что основное условие нарушается. Городу с таким свойством присвоим значение n. Он всего один, так как из остальных городов идут стрелки в n.
Далее применяем индукцию, отбрасывая город n и стрелки в него. Для оставшихся городов формируется (по предположению) единственная нумерация 1,2,...,n-1 такая, что из i в j идёт стрелка <=> i < j. Поскольку n больше всех остальных чисел, после возвращения n-го города на место всё сохранится.
Можно и без индукции. Для каждого города рассмотрим путь максимальной длины по стрелкам, оканчивающийся в данном городе. Длину такого пути ему и сопоставим. Значения могут приниматься от 0 до n-1. При этом они не повторяются: если для двух городов значения равны k, то из одного из них попадаем по ребру в другой, что увеличивает длину до k+1. Таким образом, все значения используются ровно по разу. Увеличивая их на 1, имеем описанную выше нумерацию. Ясно также, что ребро всегда идёт из i в j только при i < j.
Раскладываем на простейшие дроби с неопределенных коэффициентов:
система:
получаем: