ответ: б), в), г)
Объяснение: б) 3·(-3)² - (-3) = 30, 30 = 30 є коренем,
в) 4 + 2·( - 3) = -3 + 1, -2 = -2 є коренем
г) | - 3 | = 3, 3 = 3 є коренем
д) ( -3)² + 9 = 9 + 9= 18, 18 ≠0 , -з не є коренем рівняння
1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
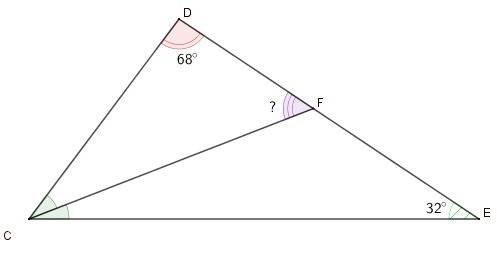
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°
1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°

x = - 3
б) 3x² - x = 30
3 * (- 3)² - (- 3) = 30
3 * 9 + 3 = 30
27 + 3 = 30
30 = 30 - верно
Является
в) 4 + 2x = x + 1
4 + 2 * ( - 3) = - 3 + 1
4 - 6 = - 2
- 2 = - 2 - верно
Является
г) | x | = 3
| - 3 | = 3 - верно
Является
д) x² + 9 = 0
(- 3)² + 9 = 0
9 + 9 = 0
18 = 0 - неверно
Не является