x=9
Объяснение:
||2x-5|-1|=x+3 ОДЗ: x+3≥0⇒x≥-3⇒x∈[-3;∞)
1)|2x-5|-1=x+3⇒|2x-5|=x+4
1.1)2x-5≥0⇒x≥2.5
2x-5=x+4⇒x=9
1.2)2x-5<0⇒x<2.5
2x-5=-x-4⇒3x=1⇒x=1/3
2)|2x-5|-1=-x-3⇒|2x-5|=-x-2
2.1)2x-5≥0⇒x≥2.5
2x-5=-x-2⇒3x=3⇒x=1⇒x∈∅
2.2)2x-5<0⇒x<2.5
2x-5=x+2⇒x=7⇒x∈∅
x={1/3;9}
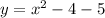
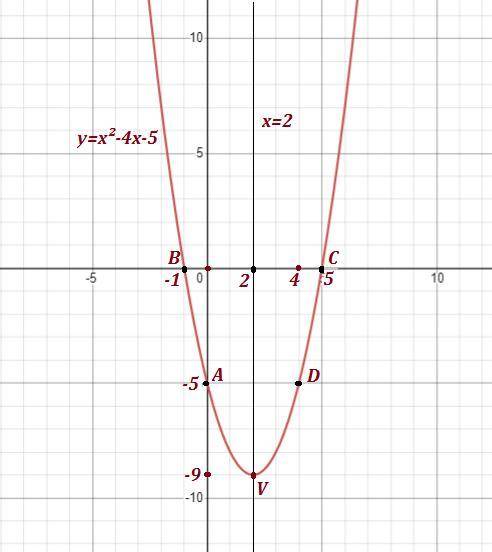
a) Найдём точки пересечения графика функции с осью ОУ. Уравнение оси ОУ: х=0.
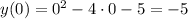
Точка пересечения графика с ОУ - точка А(0; -5) .
б) Найдём точки пересечения графика ф-ции с осью ОХ Уравнение оси ОХ: у=0.
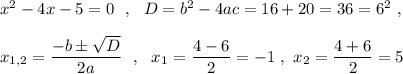
Точки пересечения графика с ОХ - точки В(1-;0) и С(5;0) .
в) Ось симметрии заданной параболы проходит через её вершину перпендикулярно оси ОХ . Найдём абсциссу вершины параболы.
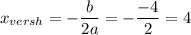
Ось симметрии - прямая х=2 .
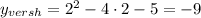, координаты вершины параболы V(2;-9) .
c) Для построения графика, можно найти координаты точки, симметричной точке А(0;-5) относительно оси х=4. Это точка D(4;-5) .
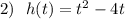
Графиком заданной функции является парабола с ветвями , направленными вверх, так как коэффициент перед t² равен 1>0 . А такая траектория движения не соответствует движению подброшенного мяча . Поэтому условие задано некорректно .
Объяснение:
Квадратное уравнение приведённое, то есть, коэффициент "а" равен 1.Для приведённого квадратного уравнения справедлива теорема Виета:
Если х₁ и х₂ – корни квадратного уравнения "x²+px+q=0", то, сумма корней равна коэффициенту "р" с противоположным знаком, т.е. "-р"; а произведение корней свободному члену "q".Найдём дискриминант уравнения, чтобы убедиться, что корни есть, или убедиться, что их нет.
Напомню, что если D>0, то квадратное уравнение имеет два корня. Если D=0, то уравнение имеет один корень. Если D<0, то действительных корней нет.Запишем коэффициенты нашего уравнения:а = 1 ; b = 5 ; c = 19.
Формула дискриминанта:D = b² – 4ac. Подставим коэффициенты в формулу. Получим, D = 5² – 4 · 1 · 19 = 25 –76 = -51. Посколько D<0, то действительных корней нет, следовательно, суммы корней тоже нет.
