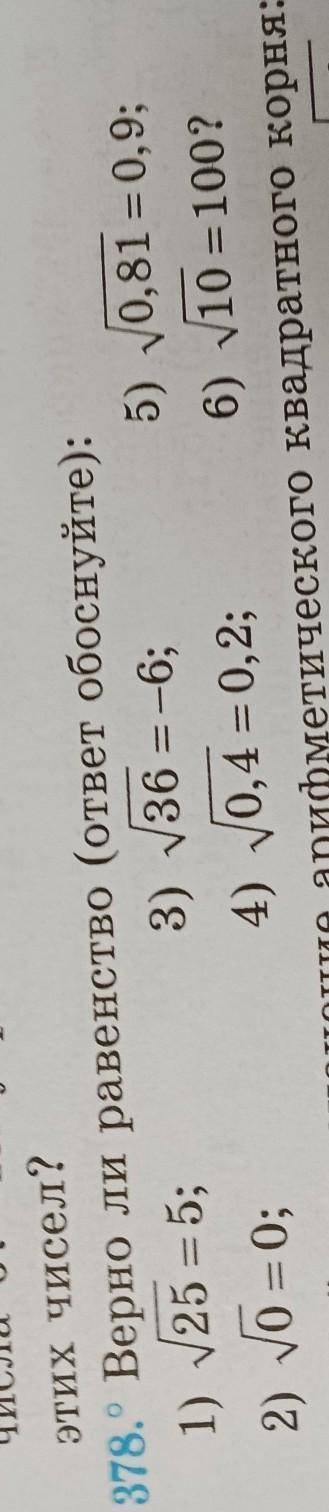
Нам нужно найти число, которое нужно возвести во вторую степень, чтобы получить то же значение, что и под корнем.
1) √ 25 = 5 - верно, так как 5^2 = 25
2) √0 = 0 - верно, так как 0^2 = 0
3) √36 = -6 - неверно, так как мы не можем из квадратного корня получить отрицательный ответ, только если перед корнем стоит -
4) √0,4 = 0,2 - неверно, так как 0,2^2 = 0,04
5) √0,81 = 0,9 - верно, так как 0,9^2 = 0,81
6) √10 = 100 - неверно, так как 100^2 = 10000
34
Объяснение:
пусть первое число 2n
а второе 2n+2
2n(2n+2)≤300
4n²+4n-300≤0 разделим на 4
n²+n-75≤0
решим методом интервалов
n²+n-75=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 1 - 4·1·(-75) = 1 + 300 = 301
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁= (-1 - √301)/ 2 ≈ -9.1747
x₂ = ( -1 + √301)/ 2 ≈ 8.1747
по свойству квадратичной функции т.к. старший коэффициент квадратного уравнения равен 1 и 1>0 ветки направлены вверх
тогда решением неравенства будет область между корнями
(x₁)(x₂)>
+ - +
n²+n-75≤0 при х∈[x₁;x₂]
так как нам требуется максимально возможная сумму последовательных четных чисел то выбираем наибольшее положительное четное число из интервала [x₁;x₂] что приближенно равно [-9.1 ;8,1]
это число n=8
тогда 2n=2*8=16 первое число
2n+2=16+2=18 второе число
16*18=288≤300
16+18=34 это максимально возможная сумма последовательных четных чисел, произведение которых не превышает 300
1) корень из 25 = 5^2=5.
ответ: да.
2) Любой корень из 0 равно 0, поэтому тоже верно.
3)Равенство неверно, т.к. две стороны с разными знаками.
4) Верно.
5) Верно.
6) Неверно, т.к. число, выходящее из корня больше самого корня