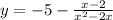
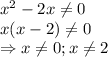
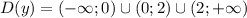
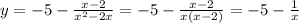
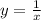, отображенную симметрично оси абсцисс и сдвинутую на 5 единиц вниз. Помним про то, что функция не определена в точках 0 и 2.
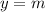представляет собой прямую, параллельную оси абсцисс, проходящую через точку (0; m). 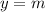не имеет общих точек с построенным графиком при 
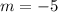(асимптота гиперболы по построению, так как сдвиг проводился на 5 единиц вниз) и при 
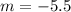(именно это значение принимала бы функция 
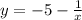в точке 2, но эта точка не принадлежит области ее определения).
Далее:
Таким образом, получаем уравнение:
Теперь понятно, что можно ввести замену
Советую запомнить приём, который я здесь употребил. Он состоит вот в чём.
Мы помним формулу сокращённого умножения:
Отсюда я могу легко выразить сумму квадратов:
Думаю, Вы уже догадались, что в нашем уравнении сыграло роль x, а что y.
Этот приём встречается очень часто в самых неожиданных ситуациях, так что рекомендую запомнить его.
Уравнение можно было решить и по формулам понижения степени(правда, это значительно было бы сложнее). Но в целом, можно рассмотреть и такой вариант, но я показал проще.
Делаем замену:
После замены получаем:
Умножаем обе части уравнения на 8t(с дробями работать крайне неудобно, да и t в знаменателе нам ни к чему - просто запомним, что он должен быть отличным от 0, а потом проверим это):
Решаем квадратное уравнение(кстати, t уже отличен от 0. В этом можно убедиться прямой подстановкой)
Следовательно, возвращаясь к переменной x, получаем простейшее уравнение:
Отсюда
Это и есть ответ. Напомню, что при решении простейшего уравнения я использовал формулу понижения степени, а в конечном результате n - целое число.