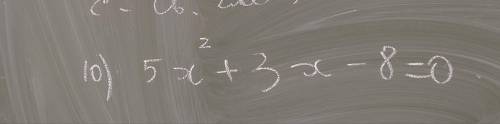
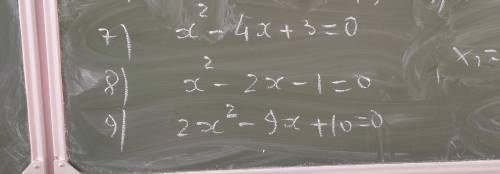
Найдем скорость часовой стрелки:
она проходит полный круг, т.е. 360° за 12 часов или за 12 · 60 = 720 минут.
Vч = 360°/720 = 0,5 (градуса в минуту)
Найдем скорость минутной стрелки:
она проходит полный круг, т.е. 360° за 1 час или за 60 минут.
Vм = 360°/60 = 6 (градусов в минуту)
Значит за 4 часа 45 мин минутная стрелка полных круга и 270°,
а часовая:
4 ч 45 мин = 4 · 60 + 45 мин = 285 мин
0,5° · 285 = 142,5°
270° - 142,5° = 127,5° - меньший из углов между стрелками.
Чтобы минутная стрелка догнала часовую первый раз, ей надо "компенсировать" расстояние между ними, т.е. больший из углов:
360° - 127,5° = 232,5°
Скорость опережения:
6 - 0,5 = 5,5 (градусов в минуту)
232,5° : 5,5 = 42 и 3/11 (мин) - время, за которое минутная стрелка первый раз догонит часовую.
Далее, расстояние между стрелками будет составлять 360°. Если разделим его на скорость опережения, найдем время, за которое минутная стрелка будет догонять часовую:
360° : 5,5 = 65 и 5/11 (мин).
Это время повторится 6 раз. Итого:
(65 и 5/11) · 6 + (42 и 3/11) = 720/11 · 6 + 465/11 = 4320/11 + 465/11 = 4785/11 = 435 мин
Объяснение:
10) 5x²+3x-8=0;
a=5; b=3; c=-8;
D=b²-4ac=3²-4*5*(-8)=9+160=169>0 --- 2 корня.
x1=(-b+√D)/2a=(-3+√169)/2*5=( -3+13)/2*5=10/10=1;
x2=(-b-√D)/2a=(-3-√169)/2*5=(-3-13)/2*5=-16/10= -1.6.
***
7) x²-4x+3=0;
По теореме Виета:
x1+x2=4;
x1*x2=3;
x1=3; x2=1;
***
x²-2x-1=0;
a=1; b=-2; c= -1;
D=b²-4ac=(-2)²-4*1*(-1)=4+4=8>0 - 2 корня.
x1=(-(-2)+√8)/2*1=(2+2√2)/2 =1+√2;
x2= (-(-2)-√8)/2=(2+2√2)/2=1-√2.
***
9) 2x²-9x+10=0;
a=2; b=-9; c=10;
D=b²-4ac=(-9)²-4*2*10=81-80=1>0 --- 2 корня.
x1=(-b+√D)/2a=(-(-9)+√1)/2*2=10/4=2.5;
x2=(-b-√D)/2a=(-(-9)-√1)/2*2=(9-1)/4=8/4=2.