912.
Сначало всё обозначим:
скорость лодки х ;
скорость лодки против чтения х-4 ;
время пути по реке 20/х-4 ;
время пути по озеру 14/х.
Разница между тем и другим временем 1 час по условию. Составляем уравнение:
20/х-4 - 14/х = 1
Приводим к общему знаменателю, перемножаем, получаем квадратное уравнение:
х^2 - 10х - 56 = 0
По формуле квадратных корней находим
х1 = - 4
отбрасываем, отрицательной скорости не бывает,
х2 = 14
принимаем, это собственная скорость лодки. Скорость лодки против течения 14 - 4 = 10 (км/ч)
914.
(знаки это дробь)
Так как скорость не может принимать отрицательное значение, следовательно искомый ответ : 40.
ответ : Токарь должен был обрабатывать 40 деталей в час по плану.
915.
Решение.
Пусть х изделий бригада должна была изготовить в 1 день по плану
(120/х) дней - бригада должна работать
(х+2) - изделия
Бригада изготовляла фактически в 1 день 120/(х+2) дней - бригада работала фактически.
А так как, по условию задачи, бригада закончила работу на 3 дня раньше срока, то составим уравнение:
120/х - 120/(х+2) = 3
120(х+2) - 120х = 3х(х+2)
120х+240 - 120х - 3х² - 6х = 0
3х² + 6х - 240 = 0
х² + 2х - 80 = 0
D = 4 + 4 × 1 × 80 = 324
x¹ = (-2 - 18)/2 = - 10 < 0 не удовлетворяет условию задачи
х² = (-2 + 18)/2 = 8
8 - изделий бригада рабочих изготовляла в 1 день по плану.
ответ : 8 изделий.
Нуу вроде всё)

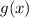 ;
; ;
; и будет искомой фигурой.
и будет искомой фигурой.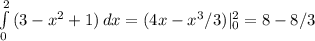
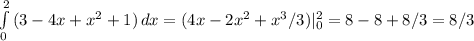
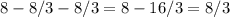 (кв. ед.)
(кв. ед.)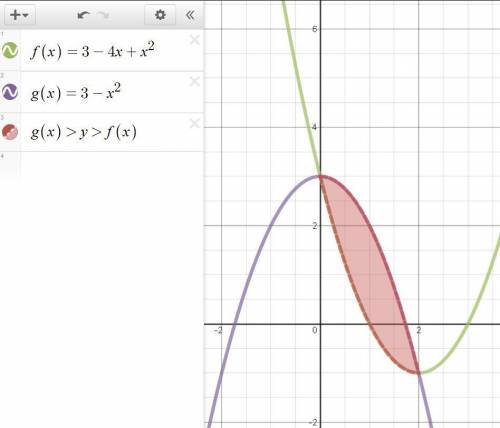
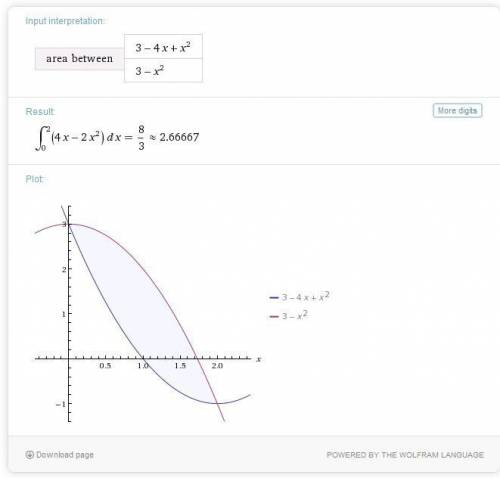
расстояние S =45 км
время до встречи t=20 мин =1/3 час
обозначим скорость
х - первый из М
y - второй из N
тогда встречная скорость x+y =S/ t ; x+y = 45 / 1/3 = 135 (1)
время движения первого от M до N
t1 =S / x
время движения второго от N до M
t2 =S / y
по условию t2 - t1 = 9 мин = 9/60 =3/20 час
S / y - S / x = 3/20 ; S (1/x -1/y) =3/20 ; 45 (1/x -1/y) =3/20 ; (1/x -1/y) = 1/300 (2)
решаем сиcтему из (1) (2)
x+y =135 ; x = 135 - y
(1/x -1/y) = 1/300 ; (1/(135-y) -1/y) = 1/300
300 (y -(135-y)) =y *(135-y)
квадратное уравнение
y^2 +465y -40500 =0
y1 = - 540 - отрицательное значение не подходит
y2 = 75 ; тогда x =135 - 75 = 60
ответ
скорость первого 60 км/ч
скорость второго 75 км/ч