1) 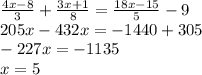
ответ: 5
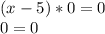
ответ : x принадлежит R
2) ответ: нет решений, т.к. графики не пересекаются
3) Составим таблицу:
1 раствор 2 раствор смесь
концентрация 8 % 16% 11%
масса х мл у мл 400 мл
масса соли х*8/100 у*16/100 400*11/100
Тогда получим два уравнения
х+у=400
0,08х+0,16у=44
Решим полученную систему:
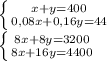
Вычтем из второго уравнения первое:
8x+16y-8x-8y=4400-3200
8y=1200
y=150 мл
Тогда х= 400-150=250 мл
ответ: Первого раствора 250 мл, второго 150 мл
Надо взять 250 мл раствора концентрации 8% и 150 мл раствора концентрации 16%
Объяснение:
Для удобства вычислений переведём %-ты в десятичные дроби:
8%=8:100=0,08
16%=16:100=0,16
11%=11:100=0,11
Пусть масса первого раствора равна х мл,
тогда масса второго раствора равна (400-х) мл.
Масса соли в первом растворе равна 0,08х мл,
масса соли во втором растворе равна 0,16(400-х) мл.
По условию, получено 400 мл раствора концентрации 11%.
Составляем уравнение:
0,08х+0,16(400-х)=0,11*400
0,08х+64-0,16х=44
-0,08х = -20
х=-20:(-0,08)
х= 250 (мл) - масса первого раствора
400-250=150 (мл) - масса второго раствора
Дана система уравнений:
{x²+xy-12y²=0
{2x²-3xy+y²=90.
Первое уравнение представим так:
x²- (3xy + 4xy) + (-3y*4y) = 0.
Это равносильно разложению на множители:
(x - 3y)(x + 4y) = 0.
Отсюда выразим у = х/3 и у = -х/4, которые подставим во второе уравнение.
Подставим у = х/3.
2x² - 3x(х/3) + (х/3)² = 90,
2x²- x²+ (x²/9)=90,
10x²= 9*90
x = ± 9.
y = ± 9/3 = ± 3.
Найдены 2 корня: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
Подставим у = -х/4.
2x² - 3x(-х/4) + (-x/4)² = 90,
2x²+ (3x²/4)+ (x²/16)=90,
32x² + 12x² + x²= 16*90.
45x²= 16*90
x = √32 = ±(4√2).
y = ± (4√2/4) = ± √2.
Найдены ещё 2 корня: х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.
ответ: х1 = -9, у1 = -3, х2 = 9, у2 = 3.
х3 = -(4√2), у1 = √2, х4 = (4√2), у4 = -√2.