
x * (x^2 + 2 * x + 1) = 2 * (x + 1);
x * (x + 1)^2 = 2 * (x + 1);
x * (x + 1)^2 - 2 * (x + 1) = 0;
(x + 1) * (x * (x + 1) - 2) = 0;
1) x + 1 = 0;
Для вычисления корня уравнения в линейном виде, нужно числа записать по одну сторону уравнения, а переменные по другую. Тогда, при переносе значений от знака равно, их знаки меняются.
x = -1;
2) x * (x + 1) - 2 = 0;
x^2 + x - 2 = 0;
Найдем дискриминант квадратного уравнения.
D = b^2 - 4 * a * c = 1 - 4 * 1 * (-2) = 9;
x1 = (-1 + 3)/2 = 2/2 = 1;
x2 = (-1 - 3)/2 = -4/2 = -2;
ответ: х = 1, х = -1 и х = -2.
x * (x^2 + 2 * x + 1) = 2 * (x + 1);
x * (x + 1)^2 = 2 * (x + 1);
x * (x + 1)^2 - 2 * (x + 1) = 0;
(x + 1) * (x * (x + 1) - 2) = 0;
1) x + 1 = 0;
Для вычисления корня уравнения в линейном виде, нужно числа записать по одну сторону уравнения, а переменные по другую. Тогда, при переносе значений от знака равно, их знаки меняются.
x = -1;
2) x * (x + 1) - 2 = 0;
x^2 + x - 2 = 0;
Найдем дискриминант квадратного уравнения.
D = b^2 - 4 * a * c = 1 - 4 * 1 * (-2) = 9;
x1 = (-1 + 3)/2 = 2/2 = 1;
x2 = (-1 - 3)/2 = -4/2 = -2;
ответ: х = 1, х = -1 и х = -2.
(0;-1) (-0,2;0) (1;0)
Объяснение:
y = 5x² - 4x - 1
ну чего уж тут.
Нули найти - значит найти у при x = 0 выходит у = -1, (0;-1) это пересечение с ОY
далее у = 0 найдем х
5x² - 4x - 1 = 0
D= 16+20 = 36
x₁ =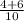 = 1, x₂ =
= 1, x₂ = 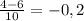
пересечение с осью OX (-0,2;0) и (1;0)