Рассматривается выражение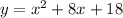 
Докажем, что y положительно при любом значении x. Допустим, что это не так. Найдём такие x, при которых y ≤ 0. Для этого решим неравенство:
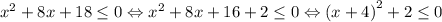
Или
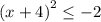
Что не имеет решений, так как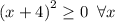 
Мы пришли к противоречию. Следовательно, 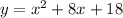принимает положительное значение при любых x.
Для нахождения наименьшего значения найдём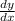 
:
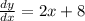
Приравняв его 0, найдём точку экстремума:
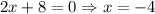
Убедимся, что найденная точка — действительно минимум.
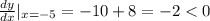
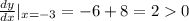
Итак, первая производная меняет в точке 
знак с "-" на "+", следовательно, в этой точке мы действительно имеем минимум.
Значение y при x = -4:
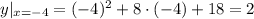
Если следовать условию задачи, то у нас получается прямоугольный треугольник, в котором АС и СВ катеты, а АВ гиппотенуза.
Синус угла А=Против катет (СВ)\Гиппотенузу(АВ)
Чтобы найти угол нужно найти катет СВ. Для этого воспользуемся теоремой пифагора. АВ в квадрате-АС в квадрате=СВ в квадрате.=> 900-576=324=> СВ в квадрате=324, значит, СВ=18
Теперь находим синус. Sin A= 18/30=0,6. Чтобы узнать градусную меру, нужно, воспользоваться таблицей Брадиса. По таблице Брадиса Sin 0,6=37 градусов.(примерно)