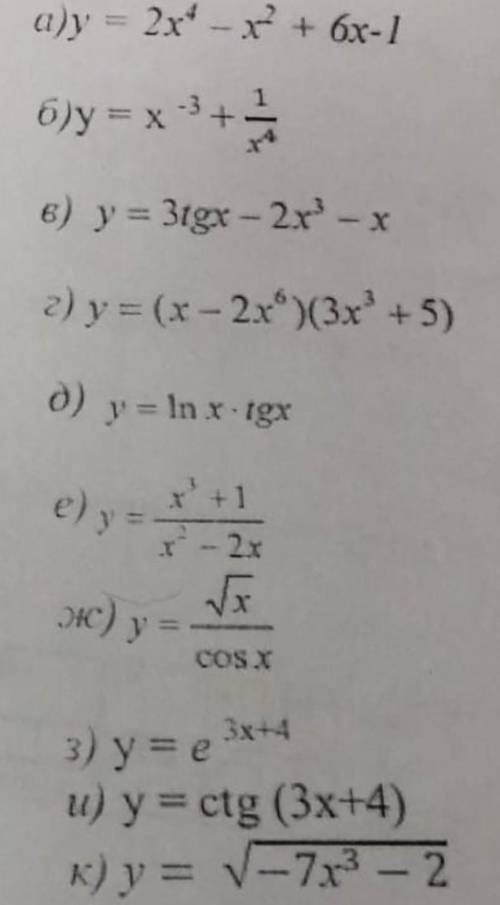
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 2x1 + x2 - 3x3 + 5x4 = 0
{ 3x1 - 2x2 + x3 - 3x4 = 0
{ 3x1 + 5x2 - 10x3 + 18x4 = 0
Умножаем 1 уравнение на -2 и складываем со 2 уравнением.
Умножаем 1 уравнение на -3 и складываем с 3 уравнением.
Умножаем 4 уравнение на -1 и складываем с 3 уравнением.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
{ 0x1 - 14x2 + 22x3 - 42x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
2, 3 и 4 уравнения все одинаковые, от них можно оставить одно.
{ x1 + 4x2 - 7x3 + 13x4 = 0
{ 0x1 - 7x2 + 11x3 - 21x4 = 0
Переменные x3 и x4 - свободные, могут быть какими угодно.
x2 = 11/7*x3 - 3x4
x1 = 7x3 - 13x4 - 4x2 = 7x3 - 13x4 - 44/7*x3 + 12x4 = 5/7*x3 - x4
Это общее решение системы.
Ненулевое решение: например, x3 = 7, x4 = 1, x2 = 8, x1 = 4
ответ:Пусть S - сумма всех чисел. Т.к. сумма чисел в каждой строке и в каждом столбце равны, то сумма одной строки или одного столбца равна .
Возьмём сумму первых двух верхних строчек, которая равна . В эту сумму входит сумма чисел верхнего левого квадрата 2х2, равная 10. Значит, сумма чисел в прямоугольнике высотой 2 и длиной 3 в верхнем правом углу равна .
Возьмём сумму нижних трёх строчек, равную , и в которую входит нижний правый квадрат 3х3 с суммой 15. Уберём из этих нижних трёх строчек квадрат 3х3. Останется прямоугольник высотой 3 и длиной 2, по площади равный верхнему прямоугольнику 2х3, и в которых суммы чисел тоже равны. В нижнем оставшемся прямоугольнике сумма чисел равна .
Приравниваем эти суммы и считаем S:
ответ: 25
ЗЫ. ответ означает, что сумма оставшихся областей равна нулю. А это в свою очередь говорит, что там либо все нули, либо есть отрицательные числа.
Объяснение: