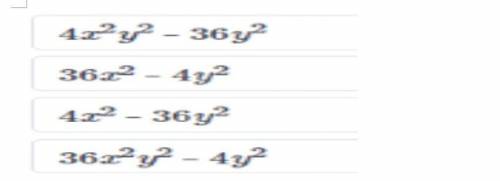
Объяснение:
1)
arccos (2x-3)=\frac{\pi }{3}arccos(2x−3)=
3
π
Так как cos(arccosx) = x, |x| \leq 1cos(arccosx)=x,∣x∣≤1 , то
\begin{gathered}2x-3 = cos\frac{\pi }{3} ;\\2x-3 = \frac{1}{2} ;\\2x=0,5+3;\\2x=3,5;\\x=3,5:2;\\x=1,75.\end{gathered}
2x−3=cos
3
π
;
2x−3=
2
1
;
2x=0,5+3;
2x=3,5;
x=3,5:2;
x=1,75.
ответ: 1,75.
2)
\begin{gathered}arccos (x+\frac{1}{3} ) =\frac{2\pi }{3} ;x+\frac{1}{3} = cos \frac{2\pi }{3} ;x+\frac{1}{3} = -\frac{1}{2} ;x=-\frac{1}{2}-\frac{1}{3};x= -\frac{5}{6} .\end{gathered}
arccos(x+
3
1
)=
3
2π
;
x+
3
1
=cos
3
2π
;
x+
3
1
=−
2
1
;
x=−
2
1
−
3
1
;
x=−
6
5
.
ответ: -\frac{5}{6} .−
6
5
.
|x-2|+|x-4|>_2
нули подмодульного выражения - это такие значения переменной х, при которых значение модуля равно нулю.
в нашем случае необходимо найти нули подмодульных выражений
|х-2| и |х-4|
х=2 х=4
х=2 х=4
||> х
|х-2|= -х+2 |х-2|= х-2 |х-2|= х-2
|х-4|= -х+4 |х-4|= -х+4 |х-4|= х-4
Значит, решаем, раскрывая модули для каждого их указанных интервалов.
|x-2|+|x-4|>_2 при х<2:
2-х+4-х>2
6-2х>2
х<2; с учетом исследуемого интервала:
х<2
|x-2|+|x-4|>_2 при 2<=х<4х-2-х+4>2
2>2 - решений на интервале нет
|x-2|+|x-4|>_2 при х>=2
x-2+x-4>2
2х>8
х>4. С учетом интервала
х>4
ответ: (-бскнчнсть;2) ; (4; +бскнчнсть)
Объяснение:
1) 4y^2(x^2-9)=4y^2(x-3)(x+3)
2) 4(9x^2-y^2)= 4(3x-y)(3x+y)
3) 4(x^2-9y^2)= 4(x-3y)(x+3y)
4) 4y^2(9x^2-1)= 4y^2(9x-1)(9x+1)
Если что, когда ставят такой значек ^ это значит, что дальше идет степень, тоесть y^2 это "у в квадрате"