у = kx + b
так как график проходит через начало координат, b = 0.
подставим координаты точки М в уравнение
4 = k * (-2.5)
Отсюда найдем k = 4/(-2.5) = -1.6
то есть искомая формула линейной функции у = -1,6х
Теперь, чтоб найти точку пересечения этого графика с прямой 3х-2у - 16 = 0, решим систему из 2 линейных уравнений
у = -1,6х
3х-2у - 16 = 0
подставив у из первого уравнения во второе, получим
3х + 3,2х - 16 = 0
6,2х = 16
х = 16/6,2= 80/31
тогда у = -1,6 *80/31 = -128/31
То есть искомая точка пересечения (80/31; -128/31)
Объяснение:
1) (7x-5)x=1,5-2,1x |×10
70x²-50x-15+21x=0
70x²-29x-15=0; D=841+4200=5041
x₁=(29-71)/140=-42/140=-3/10=-0,3
x₂=(29+71)/140=100/140=5/7
ответ: -0,3; 5/7.
2) (1-8x)x=11,2x-1,4 |×10/2
5x-40x²-56x+7=0
40x²+51x-7=0; D=2601+1120=3721
x₁=(-51-61)/80=-112/80=-7/5=-1,4
x₂=(-51+61)/80=10/80=1/8=0,125
ответ: -1,4; 0,125.
3) (1,7x -1/3)x=(3-15,3x)·1/2
2x((5,1x)/3 -1/3)=3-15,3x
10,2x²-2x=3(3-15,3x)
10,2x²-2x=9-45,9x |×10
102x²-20x-90+459x=0
102x²+439x-90=0; D=192721+36720=229441
x₁=(-439-479)/204=-918/204=-9/2=-4,5
x₂=(-439+479)/204=40/204=10/51
ответ: -4,5; 10/51.
4) (x/7 -1 6/7)x=(3,9-0,3x)·1/35
35x(x/7 -13/7)=3,9-0,3x
5x²-65x=3,9-0,3x |×10
50x²-650x-39+3x=0
50x²-647x-39=0; D=418609+7800=426409
x₁=(647-653)/100=-6/100=-0,06
x₂=(647+653)/100=1300/100=13
ответ: -0,06; 13.
Объяснение:
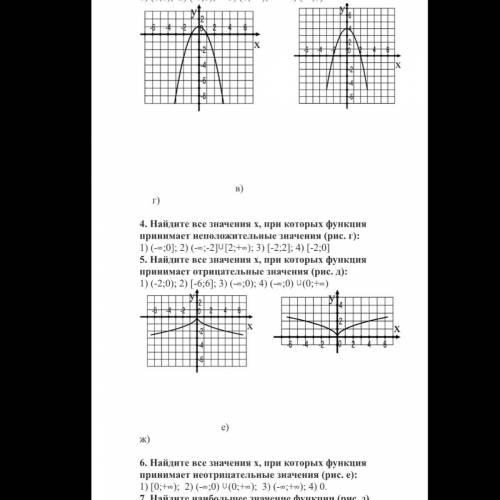
На 4 вопрос ответ 2
Для пятого вопроса нужен рисунок д, не знаю, почему его нет
На 6 вопрос ответ 4, если считать, что левый рисунок - это рисунок е
А если считать, что правый рисунок - это рисунок е, тогда на 6 вопрос ответ будет 3.
Но, судя по предыдущим рисункам, на 6 вопрос ответ все-же 4.