Объяснение:
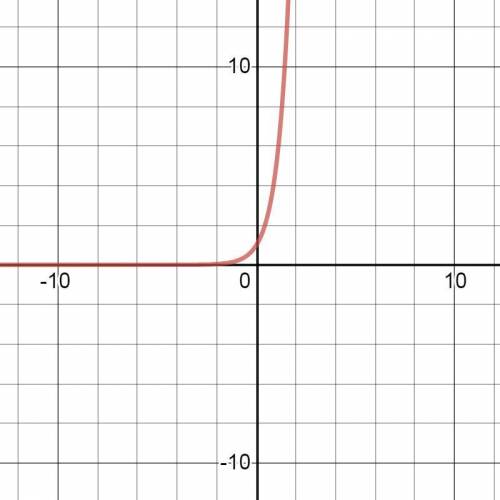
y=5ˣ.
Это показательная функция.
График этой функции показан на рис. 1.
Показательная функция y=5ˣ является строго монотонно возрастающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
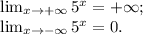
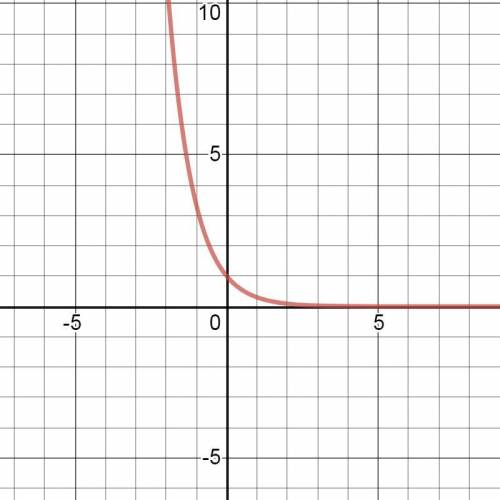
у=0,3ˣ
Это показательная функция.
График этой функции показан на рис. 2.
Показательная функция у=0,3ˣ является строго монотонно убывающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
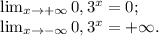
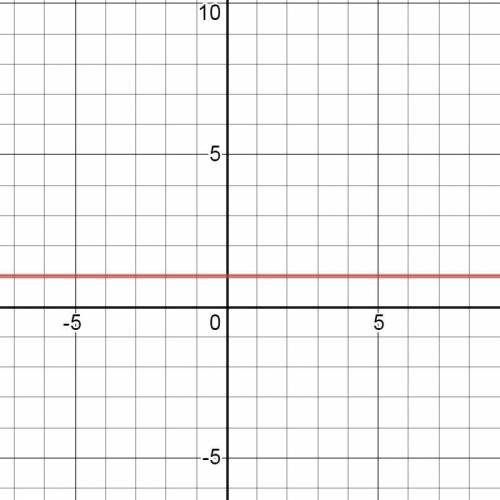
у=1ˣ.
График этой функции показан на рис. 3.
Единица в любой степени равена единице. ⇒
Получаем функцию у=1.
Графиком этой функции является график функции у=0 (ось ОХ),
смещённый вверх по оси ОУ на одну единицу.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у=1.
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
В решении.
Объяснение:
1) -2х+19=5х-16
-2х-5х= -16-19
-7х= -35
х= -35/-7
х=5
(5; 1)
2) 8х-25 =3х+20
8х-3х=20+25
5х=45
х=45/5
х=9
(9; 0)
3) 6-у=3(3у-8)
6-у=9у-24
-у-9у= -24-6
-10у= -30
у= -30/-10
у=3
(5; 3)
4) 5(у+1,2)=7у+4
5у+6=7у+4
5у-7у=4-6
-2у= -2
у= -2/-2
у=1
(1; 1)
5) 4(х-3)-16=5(х-5)
4х-12-16=5х-25
4х-5х= -25+28
-х=3
х=3/-1
х= -3
(-3; 3)
6) 3х-17=8х+18
3х-8х=18+17
-5х=35
х=35/-5
х= -7
(-7; 0)
7) 11-5у=12-6у
-5у+6у=12-11
у=1
(-3; 1)
8) 4у+(11,8-у)=3,8-5у
4у+11,8-у=3,8-5у
3у+5у=3,8-11,8
8у= -8
у= -8/8
у= -1
(1; -1)
9) 3х+16=8х-9
3х-8х= -9-16
-5х= -25
х= -25/-5
х=5
(5; 1).
(Соединять точки нужно в порядке вычислений, получится вытянуто-приплюснутая буква М)
Первая площадь круга будет равна
S1 кр=π*R^2
Первая площадь квадрата равна при D-диагональ квадрата
и D=2R
S1 кв=D^2/2=2R^2
Вторая площадь круга
радиус второго круга будет равен R*√2/2, а его площадь:
S2 кр=1/2π*R^2
Для квадрата
S2 кв=R^2
и так далее
Сумма площадей всех кругов:
Sn кругов=π*R^2+π*R^2/2+π*R^2/4+π*R^2/8+...+
+π*R^2/n=π*R^2(1+1/2+1/4+1/8+...+1/n)
Сумма площадей всех квадратов
Sn квадратов=2R^2+R^2+2R^2/2+2R^2/4+2R^2/8+...+
+2R^2/n=R^2(2+1+1/2+1/4+1/8+...+1/n)
Известно, что предел суммы ряда (1/2+1/4+1/8+...+1/n) при n ⇒∞ равен 1, тогда предел общей суммы кругов:
limS кр=π*R^2(1+1/2+1/4+1/8+...+1/n)=π*R^2(1+1)=2π*R^2
и для квадратов:
limSкв=R^2(2+1+1/2+1/4+1/8+...+1/n)=R^2(3+1)=4R^2
По-моему так.